为了解某班学生每周做家务劳动的时间,某综合实践活动小组对该班50名学生进行了调查,有关数据如下表:
| 每周做家务的时间(小时) |
0 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
| 人数(人) |
2 |
2 |
6 |
8 |
12 |
13 |
4 |
3 |
根据上表中的数据,回答下列问题:
(1)该班学生每周做家务劳动的平均时间应是多少小时?
(2)这组数据的中位数、众数分别是多少?
(3)请你根据(1)、(2)的结果,用一句话谈谈自己的感受.
如图:△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D,
(1)若△BCD的周长为8,求BC的长;
(2)若BC=4,求△BCD的周长.
如图,方格纸中的每个小方格都是边长为1的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,A(-1,5),B(-1,0),C(-4,3).
(1)画出△ABC关于y轴对称的△A1B1C1;(其中A1、B1、C1是A、B、C的对应点,不写画法)
(2)写出A1、B1、C1的坐标;
(3)求出△A1B1C1的面积.
在Rt△ABC中,∠BAC=90°,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.问△AEF与△DEB全等吗?说明理由。

根据图中尺规作图的痕迹,先判断得出结论: .
然后证明你的结论(不要求写出已知、求证).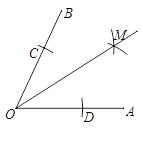
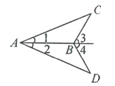
如图,∠1=∠2,∠3=∠4,求证:AC=AD.