已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△ ,使得平面
,使得平面 ⊥平面ABD.
⊥平面ABD.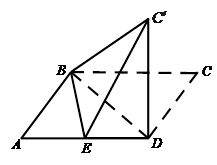
(Ⅰ)求证: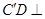 平面ABD;
平面ABD;
(Ⅱ)求直线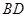 与平面
与平面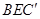 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求二面角 的余弦值.
的余弦值.
春节期间,某商场决定从3种服装、2种家电、3种日用品中,选出3种商品进行促销活动。
⑴试求选出的3种商品中至少有一种是家电的概率;
⑵商场对选出的某商品采用抽奖方式进行促销,即在该商品现价的基础上将价格提高100元,规定购买该商品的顾客有3次抽奖的机会:若中一次奖,则获得数额为 元的奖金;若中两次奖,则共获得数额为
元的奖金;若中两次奖,则共获得数额为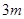 元的奖金;若中3次奖,则共获得数额为
元的奖金;若中3次奖,则共获得数额为 元的奖金。假设顾客每次抽奖中获的概率都是
元的奖金。假设顾客每次抽奖中获的概率都是 ,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?
,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?
已知向量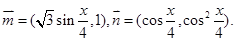 记
记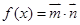 .
.
(Ⅰ)若 ,求
,求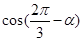 的值;
的值;
(Ⅱ)在△ABC中,角A、B、C的对边分别是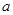 、
、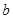 、
、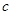 ,且满足
,且满足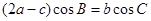 ,若
,若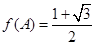 ,试判断△ABC的形状.
,试判断△ABC的形状.
在△ABC中,a、b、c分别是角A、B、C的对边,且 =-
=- .
.
(2)若b= ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.
(1) 已知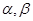 都为锐角,
都为锐角,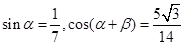 ,求
,求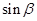 与
与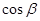 的值
的值
(2)已知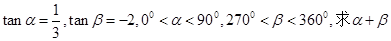 的值
的值