如图，在平面直角坐标系中，已知点A坐标为（2，4），直线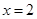
与
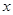轴相交于点B，连结OA，抛物线
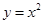从点O沿OA方向平移，与直线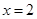交于点P，顶点M到A点时停止移动．
（1）求线段OA所在直线的函数解析式；
（2）设抛物线顶点M的横坐标为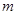
,①用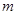的代数式表示点P的坐标；②当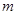为何值时，线段PB最短；
（3）当线段PB最短时，相应的抛物线上是否存在异于M的点Q，使△PQA的面积与△PMA的面积相等，若存在，请求出点Q的坐标；若不存在，请说明理由．
学校计划选购甲、乙两种图书作为“校园读书节”的奖品．已知甲图书的单价是乙图书单价的1．5倍；用600元单独购买甲种图书比单独购买乙种图书要少10本．
（1）甲、乙两种图书的单价分别为多少元？
（2）若学校计划购买这两种图书共40本，且投入的经费不超过1050元，要使购买的甲种图书数量不少于乙种图书的数量，则共有几种购买方案？
如图，CD是⊙O的直径，且CD=2cm，点P为CD的延长线上一点，过点P作⊙O的切线PA，PB，切点分别为点A，B．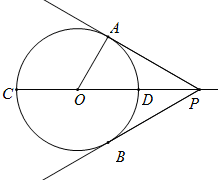
（1）连接AC，若∠APO=30°，试证明△ACP是等腰三角形；
（2）填空：
①当DP=cm时，四边形AOBD是菱形；
②当DP=cm时，四边形AOBP是正方形．
请将式子：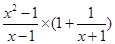
化简后，再选择一个合适的x的值代入求值．
（1）计算：（-2011）0+（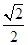
）-1+|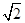
-2|-2cos60°；
（2）解方程：（2x-1）2=x（3x+2）-7．
如图，抛物线y=ax2+bx-4a经过A（-1，0）、C（0，4）两点，与x轴交于另一点B．
（1）求抛物线的解析式；
（2）已知点D（m，m+1）在第一象限的抛物线上，求点D关于直线BC对称的点的坐标；
（3）在（2）的条件下，连接BD，点P为抛物线上一点，且∠DBP=45°，求点P的坐标．