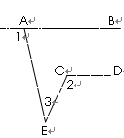
画图：⑴马小虎准备制作一个封闭的正方体盒子，他先用5个大小一样的正方形制成如下图所示的拼接图形(实线部分)，经折叠后发现还少一个面，请你在右图中的拼接图形上再接一个正方形，使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子。
(注：①只需添加一个符合要求的正方形；
②添加的正方形用阴影表示。)
⑵如图是一些小正方块所搭几何体的俯视图，小正方块中的数字表示该位置的小方块的个数，请画出这个几何体的主视图和左视图：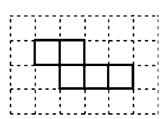
①已知
求
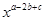的值。
②若n满足(n-2010)2+(2011-n)2=3，求(n-2010)(2011-n)的值。
③已知：多项式
中不含xy项．
求: 
的值、
观察下列各式：（x-1）(x+1)=x
–1
(x-1)(x+x+1)=x
-1
(x-1)(x+x+x+1)=x
-1
(x-1)(x+x+x+x+1)=x
-1
(1) 根据前面各式的规律可得：（x-1）(x
+x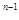
+…+x+1)= 、(其中n为正整数)
（2）根据（1）求：1+2+2+2+…+2
+2
的值，并求出它的个位数字。
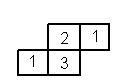
如图，给出下列论断：① DE= CE②∠1=∠2③∠3=∠4请你将其中的两个作为条件，另一个作为能成立的结论，并加以说明。（完成一种情况即可）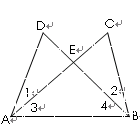
袋中有红色和黄色两种球：
①若红色球有10个，黄色球有5个，那么从袋中摸出一个球是红颜色的可能性P是多少？②若黄色球有5个，如何配置袋中的红色球使摸出的黄色球的概率为25%？
如图，AB∥CD, 请你用一个等式来表示图中∠1、∠2、∠3 这三个角之间的关系，并说明理由。