如图, 在平面直角坐标系 中, 点
中, 点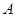 (0,8), 点
(0,8), 点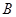 (6 , 8 ).
(6 , 8 ).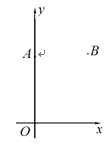
(1)只用直尺(没有刻度)和圆规, 求作一个点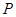 ,使点
,使点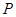 同时满足下列两个条件:(要求保留作图痕迹, 不必写出作法):
同时满足下列两个条件:(要求保留作图痕迹, 不必写出作法):
①点P到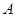 、
、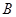 两点的距离相等;②点P到
两点的距离相等;②点P到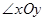 的两边的距离相等.
的两边的距离相等.
(2) 在(1)作出点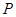 后, 在图上写出点
后, 在图上写出点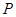 的坐标.
的坐标.
如图,C在线段BD上,△ABC和△CDE都是等边三角形,BE与AD有什么关系?请用旋转的性质证明你的结论。(不用旋转性质证明的扣1分)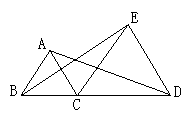
化简求值:已知 ,
, ,是方程
,是方程 的两个根,求代数式
的两个根,求代数式 的值。
的值。
矩形OABC在平面直角坐标系中的位置如图所示,A、C两点的坐标分别为A(6,0)、C(0,3),直线 与BC边相交于点D.
与BC边相交于点D.
(1)求点D的坐标;
(2)若抛物线 经过A、D两点,试确定此抛物线的解析式;
经过A、D两点,试确定此抛物线的解析式;
(3)设(2)中的抛物线的对称轴与直线AD交于点M,点P为对称轴上一动点,以P、A、M为顶点的三角形与△ABD相似,求符合条件的所有点P的坐标.
如图,四边形 、
、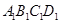 是两个边长分别为5和1且中心重合的正方形.其中,正方形
是两个边长分别为5和1且中心重合的正方形.其中,正方形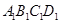 可以绕中心
可以绕中心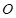 旋转,正方形
旋转,正方形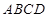 静止不动.
静止不动.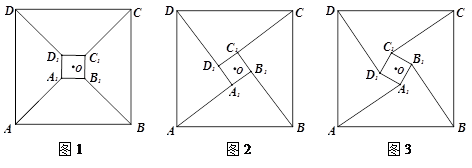
(1)如图1,当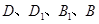 四点共线时,四边形
四点共线时,四边形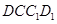 的面积为__;
的面积为__;
(2)如图2,当 三点共线时,请直接写出
三点共线时,请直接写出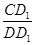 = _________;
= _________;
(3)在正方形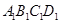 绕中心
绕中心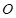 旋转的过程中,直线
旋转的过程中,直线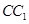 与直线
与直线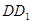 的位置关系______________,请借助图3证明你的猜想.
的位置关系______________,请借助图3证明你的猜想.
已知抛物线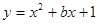 的顶点在x轴上,且与y轴交于A点. 直线
的顶点在x轴上,且与y轴交于A点. 直线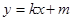 经过A、B两点,点B的坐标为(3,4).
经过A、B两点,点B的坐标为(3,4).
(1)求抛物线的解析式,并判断点B是否在抛物线上;
(2)如果点B在抛物线上,P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于点E,设线段PE的长为h,点P的横坐标为x.当x为何值时,h取得最大值,求出这时的h值.