在一次数学实践探究活动中,小强用两条直线把平行四边形ABCD分割成四个部分,使含有一组对顶角的两个图形全等;
( 1 )根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有 组;
( 2 )请在图中的三个平行四边形中画出满足小强分割方法的直线;
( 3 )由上述实验操作过程,你发现所画的两条直线有什么规律?
某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨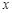 元(
元(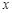 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为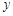 元.
元.
(1)求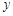 与
与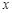 的函数关系式,并直接写出自变量
的函数关系式,并直接写出自变量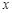 的取值范围;
的取值范围;
(2)若每个月的利润为2200元,求每件商品的售价应定为多少元?
(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大利润是多少元?
已知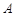 、
、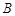 、
、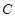 三点均在
三点均在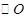 上,且
上,且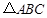 是等边三角形.
是等边三角形.
(1)如图,用直尺和圆规作出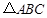 ;(不写作法,保留作图痕迹)
;(不写作法,保留作图痕迹)
(2)若点 是
是 上一点,连接
上一点,连接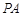 、
、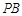 、
、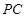 .探究
.探究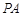 、
、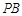 、
、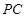 之间的等量关系并说明理由.
之间的等量关系并说明理由.
【童话故事】“龟兔赛跑”:兔子和乌龟同时从起点出发,比赛跑步,领先的兔子看着缓慢爬行的乌龟,骄傲起来,在路边的小树下睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟已先到达终点.
【数学探究】
我们假设乌龟、兔子的速度及赛场均保持不变,小莉用图1刻画了“龟兔赛跑”的故事,其中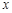 表示乌龟从起点出发所行的时间,
表示乌龟从起点出发所行的时间,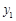 (米)表示兔子所行的路程,
(米)表示兔子所行的路程, (米)表示乌龟所行的路程.
(米)表示乌龟所行的路程.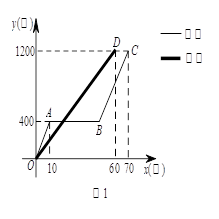
(1)分别求线段 、
、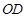 所表示的
所表示的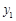 、
、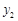 与
与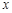 之间的函数关系式;
之间的函数关系式;
(2)试解释图中线段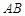 的实际意义;
的实际意义;
(3)兔子输了比赛,心里很不服气,它们约定再次赛跑,
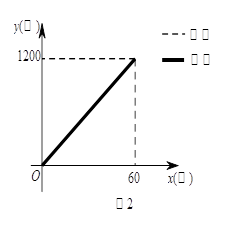
①如果兔子让乌龟先跑30分钟,它才开始追赶,请在图2中画出兔子所行的路程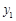 与
与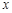 之间的函数关系的图象,并直接判断谁先到达终点;
之间的函数关系的图象,并直接判断谁先到达终点;
②如果兔子让乌龟从路边小树处(兔子第一次睡觉的地方)起跑,它们同时出发,这一次谁先到达终点呢?为什么?
“五一”节,小莉和同学一起到游乐场玩,游乐场的大型摩天轮的半径为20m,匀速旋转1周需要12min.小莉乘坐最底部的车厢(离地面0. 5m)开始1周的观光,5min后小莉离地面的高度是多少?
(精确到0.1m,下列数据供参考: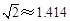 ;
;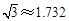 ;
;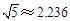 )
)

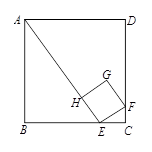
如图,正方形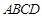 的边长为12,其内部有一个小正方形
的边长为12,其内部有一个小正方形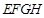 ,其中
,其中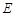 、
、 、
、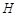 分别在
分别在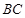
 、
、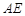 上.若
上.若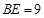 ,求小正方形
,求小正方形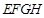 的边长.
的边长.