如图所示,水平面上有一个倾角为θ=30°的斜劈,质量为m。一个光滑小球,质量也为m,用绳子悬挂起来,绳子与斜面的夹角为a=30°,整个系统处于静止状态。
(1)求出绳子的拉力T;
(2)若地面对斜劈的最大静摩擦力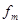 等于地面对斜劈的支持力的k倍,为了使整个系统始终保持静止,k值必须满足什么条件?
等于地面对斜劈的支持力的k倍,为了使整个系统始终保持静止,k值必须满足什么条件?
如图所示,甲图为一段粗细均匀的新型导电材料棒,现测量该材料的电阻率。
(1)首先用多用电表的欧姆档(倍率为×10)粗测其电阻,指针位置如图乙所示,其读数R=。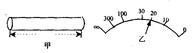
(2)然后用以下器材用伏安法尽可能精确地测量其电阻:
| A.电流表:量程为0.6 A,内阻约为0.1Ω |
| B.电压表:量程为3V,内阻约为3kΩ |
| C.滑动变阻器:最大阻值为20Ω,额定电流1A |
| D.低压直流电源:电压6V,内阻忽略 |
E.电键S,导线若干
在方框中画出实验电路图。
(3)如果实验中电流表示数为I,电压表示数为U,并测出该棒的长度为L、直径为d,则该材料的电阻率 (用测出的物理量的符号表示)。
(用测出的物理量的符号表示)。
有一个标有“2 V,24 W”的灯泡,为了测定它在不同电压下的实际功率和额定电压下的功率,需测定灯泡两端的电压和通过灯泡的电流,现有如下器材:
| A.直流电源15V(内阻可不计) |
| B.直流电流表0~0.6 A~3A(内阻0.5Ω、0.1Ω) |
| C.直流电流表0~300 mA(内阻约5Ω) |
| D.直流电压表0~3V~15(内阻约3 kΩ、15 kΩ) |
E.直流电压表0~25 V(内阻约200 kΩ)
F.滑动变阻器10Ω、5 A
G.滑动变阻器1kΩ、3 A
(1)实验台上已放置开关、导线若干及灯泡,为了完成实验需要从上述器材中再选用(用序号字母表示) 。
(2)在答案卷上相应方框内画出最合理的实验电路图。
(3)若测得灯丝电阻R随灯泡两端电压变化关系的图线如图所示,由这条曲线可得出:正常发光条件下,灯丝消耗的电功率是 。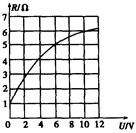
(4)如果灯丝电阻与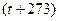 的大小成正比,其中t为灯丝摄氏温度值,室温t=27℃,则正常发光时灯丝的温度是 ℃。
的大小成正比,其中t为灯丝摄氏温度值,室温t=27℃,则正常发光时灯丝的温度是 ℃。
电源的输出功率P跟外电路的电阻R有关。如图所示,是研究它们关系的实验电路。为了便于进行实验和保护蓄电池,给蓄电池串联了一个定值电阻R0,把它们一起看作新电源(图中虚线框内部分)。新电源的内电阻就是蓄电池的内电阻和定值电阻R0之和,用r表示,电源的电动势用E表示。
①写出新电源的输出功率P跟E、r、R的关系式:。(安培表、伏特表看作理想电表)。
②在实物图中按电路图画出连线,组成实验电路。
③表中给出了6组实验数据,根据这些数据,在方格纸中画出P-R关系图线。根据图线可知,新电源输出功率的最大值约是W,当时对应的外电阻约是.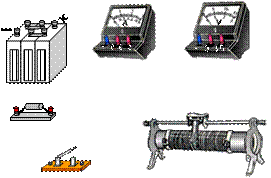 ④由表中所给出的数据,还可以求哪些物理量?
④由表中所给出的数据,还可以求哪些物理量?
| U(V) |
3.5 |
3.0 |
2.5 |
2.0 |
1.5 |
1.0 |
| I(A) |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |

在做“用单摆测定重力加速度”的实验时,已知摆球直径为2.00cm,让刻度尺的零刻线对准摆线的悬点,摆线竖直下垂,如图,则单摆摆长是______m;某次实验测定40次全振动的时间如图中秒表所示,则单摆周期是______s,本次实验测得重力加速度g=________m/s2.
①在“长度的测量”实验中,调整游标卡尺两侧脚间距离,主尺和游标的位置如图所示,此时卡尺两脚间狭缝宽度为_______mm;若要狭缝宽度调到0.20mm,应使游标上除0刻度线外第_______条刻度线与主尺上表示_________mm的刻度线对齐。
 |
②如图所示,螺旋测微器测出的金属丝的直径是__________mm.