如图,货轮在海上以35n mile / h的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为 的方向航行.为了确定船位,在B点观察灯塔A的方位角是
的方向航行.为了确定船位,在B点观察灯塔A的方位角是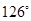 ,航行半小时后到达C点,观察灯塔A的方位角是
,航行半小时后到达C点,观察灯塔A的方位角是 .求货轮到达C点时与灯塔A的距离(精确到1 n mile).
.求货轮到达C点时与灯塔A的距离(精确到1 n mile).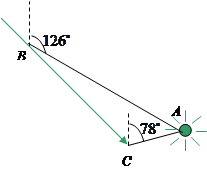
14分)已知在数列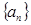 中,
中,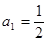 ,
,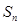 是其前
是其前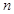 项和,且
项和,且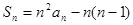 .
.
(1)证明:数列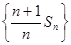 是等差数列;
是等差数列;
(2)令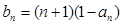 ,记数列
,记数列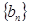 的前
的前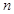 项和为
项和为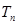 .
.
①;求证:当 时,
时,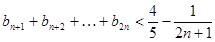
②: 求证:当 时,
时,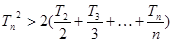
已知函数 ,
,
(1)求函数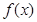 的单调区间;
的单调区间;
(2)若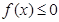 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
(3)证明: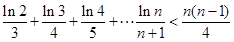 (
( 且
且 )
)
(本小题满分12分)
椭圆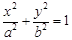
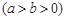 过点
过点 ,其左、右焦点分别为
,其左、右焦点分别为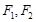 ,离心率
,离心率 ,
,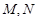 是直线
是直线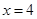 上的两个动点,且
上的两个动点,且 .
.
(1)求椭圆的方程;(2)求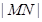 的最小值;
的最小值;
(3)以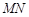 为直径的圆
为直径的圆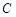 是否过定点?请证明你的结论.
是否过定点?请证明你的结论.
.某市环保研究所对市中心每天环境污染情况进行调查研究后,发现一天中环境综合污染指数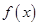 与时间x(小时)的关系为
与时间x(小时)的关系为 ,其中
,其中 是与气象有关的参数,且
是与气象有关的参数,且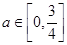 ,若用每天
,若用每天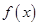 的最大值为当天的综合污染指数,并记作
的最大值为当天的综合污染指数,并记作 .
.
(1)令 ,求t的取值范围;(2)求函数
,求t的取值范围;(2)求函数 ;
;
(3)市政府规定,每天的综合污染指数不得超过2,试问目前市中心的综合污染是否超标?请说明理由。
如右图,已知AB⊥平面ACD,DE⊥平面ACD,
△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(1)求证:AF∥平面BCE;
(2)求直线BF和平面BCE所成角的正弦值