设等差数列 的第10项为23,第25项为
的第10项为23,第25项为 ,求:
,求:
(1)数列 的通项公式; (2)数列
的通项公式; (2)数列 前50项的绝对值之和。
前50项的绝对值之和。
圆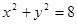 内有一点
内有一点 ,
,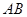 为过点
为过点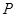 且倾斜角为
且倾斜角为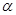 的弦,
的弦,
(1)当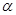 =1350时,求
=1350时,求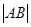 ;
;
(2)当弦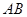 被点
被点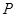 平分时,求出直线
平分时,求出直线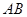 的方程;
的方程;
(3)设过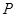 点的弦的中点为
点的弦的中点为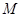 ,求点
,求点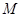 的坐标所满足的关系式.
的坐标所满足的关系式.
已知多面体ABCDFE中, 四边形ABCD为矩形,AB∥EF,AF⊥BF,平面ABEF⊥平面ABCD, O、M分别为AB、FC的中点,且AB = 2,AD =" EF" = 1.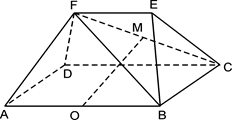
(1)求证:AF⊥平面FBC;
(2)求证:OM∥平面DAF;
(3)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为VF-ABCD,VF-CBE,求VF-ABCD∶VF-CBE的值.
已知 中,顶点
中,顶点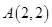 ,边
,边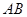 上的中线
上的中线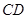 所在直线的方程是
所在直线的方程是 ,边
,边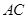 上高
上高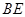 所在直线的方程是
所在直线的方程是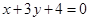 .
.
(1)求点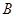 、C的坐标;(2)求
、C的坐标;(2)求 的外接圆的方程.
的外接圆的方程.
设全集为 ,集合
,集合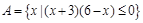 ,
, .
.
(1)求如图阴影部分表示的集合;
(2)已知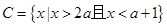 ,若
,若 ,求实数
,求实数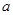 的取值范围.
的取值范围.
已知直线l经过直线3x+4y-2=0与直线2x+y+2=0的交点P,且垂直于直线x-2y-1=0 .
(1)求直线l的方程;(2)求直线l关于原点O对称的直线方程。