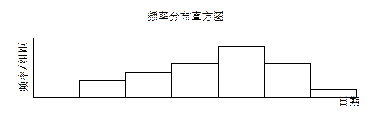某公司要将一批不易存放的蔬菜从 地运到
地运到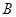 地,有汽车、火车两种运输工具可供选择,两种运输工具的主要参考数据如下表:
地,有汽车、火车两种运输工具可供选择,两种运输工具的主要参考数据如下表:
| 运输工具 |
途中速度 (千米/小时) |
途中单位费用(元/千米) |
装卸时间 (小时) |
装卸费用(元) |
| 汽车 |
50 |
8 |
2 |
1000 |
| 火车 |
100 |
4 |
4 |
2000 |
若这批蔬菜在运输过程中(含装卸时间)损耗为300元/小时,设 、
、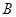 两地距离为
两地距离为 千米.
千米.
(1)设采用汽车与火车运输的总费用分别为 与
与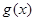 ,求
,求 与
与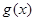 的解析式;
的解析式;
(2)试根据 、
、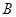 两地距离的大小比较采用哪种运输工具更合算(即运输总费用最小).(注:总费用=途中费用+装卸费用+损耗费用)
两地距离的大小比较采用哪种运输工具更合算(即运输总费用最小).(注:总费用=途中费用+装卸费用+损耗费用)
(1)化简: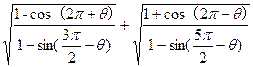
(2)求值: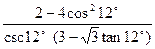
在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点.已知|AB|=2|OA|,且点B的纵坐标大于零.
(1)求向量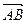 的坐标;
的坐标;
(2)求圆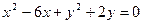 关于直线OB对称的圆的方程;
关于直线OB对称的圆的方程;
(3)是否存在实数a,使函数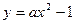 的图像上总有关于直线OB对称的两个点?若不存在,说明理由:若存在,求a的取值范围.
的图像上总有关于直线OB对称的两个点?若不存在,说明理由:若存在,求a的取值范围.
(题满分12) 已知
(1)化简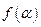 ;(2)若
;(2)若 ,求
,求
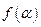 的值.[
的值.[
( (本小题满分10分)已知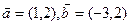
①若 与
与 垂直,
垂直, 求k的值
求k的值
②若 与
与 平行,求k的值
平行,求k的值
评委会把同学们上 交的作品的件数按5天一组分组统计,绘制了频率分布直方图,如图所示,已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为 12 ,请解答下列问题:
交的作品的件数按5天一组分组统计,绘制了频率分布直方图,如图所示,已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为 12 ,请解答下列问题:
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组的获奖率高?
|