(本小题满分12分)如图所示,某小区为美化环境,准备在小区内草坪的一侧修建一条直路OC;另一侧修建一条休闲大道,它的前一段OD是函数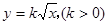 的一部分,后一段DBC是函数
的一部分,后一段DBC是函数 时的图象,图象的最高点为
时的图象,图象的最高点为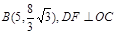 ,垂足为F.
,垂足为F.
(1)求函数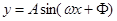 的解析式;
的解析式;
(2)若在草坪内修建如图所示的儿童游乐园PMFE,问点P落在曲线OD上何处时,儿童乐园的面积最大?
甲乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如 下,
下,
甲运动员
| 射击环数 |
频数 |
频率 |
| 7 |
10 |
0.1 |
| 8 |
10 |
0.1 |
| 9 |
 |
0.45 |
| 10 |
35 |
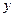 |
| 合计 |
 100 100 |
1 |
乙运动员
| 射击环数 |
频数 |
频率 |
| 7 |
8 |
0.1 |
| 8 |
12 |
0.15 |
| 9 |
 |
|
| 10 |
0.35 |
|
| 合计 |
80 |
1 |
若将频率视为概率,回答下列问题,
(1)求甲运动员击中10环的概率
(2)求甲运动员在3次射击中至少有一次击中9环以上(含9环)的概率
(3)若甲运动员射击2次,乙运动员射击1次, 表示这3次射击中击中9环以上(含9环)的次数,求
表示这3次射击中击中9环以上(含9环)的次数,求 的分布列及
的分布列及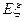 .
.
设 的内角
的内角 所对的边分别为
所对的边分别为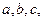 且
且 .
.
(1)求角 的大小;
的大小;
(2)若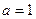 ,求
,求 的周长
的周长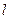 的取值范围.
的取值范围.
(本题满分12分)已知函数 (
(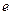 为自然对数的底数).
为自然对数的底数).
(1)求函数 的最小值;
的最小值;
(2)若 ,证明:
,证明: .
.
(本题满分14分)设有抛物线C: ,通过原点O作C的切线
,通过原点O作C的切线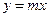 ,使切点P在第一象限.
,使切点P在第一象限.
(1)求m的值,以及P的坐标;
(2)过点P作切线的垂线,求它与抛物线的另一个交点Q;
(3)设C上有一点R,其横坐标为 ,为使DOPQ的面积小于DPQR的面积,试求
,为使DOPQ的面积小于DPQR的面积,试求 的取值范围.
的取值范围.
(本题满分14分)已知函数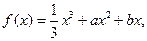 且
且

(1)试用含 的代数式表示
的代数式表示 ;
;
(2)求 的单调区间.
的单调区间.