(本小题满分14分)
为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
|
5 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为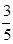
．
（1）请将上面的列联表补充完整(不用写计算过程)；
（2）能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关？说明你的理由；
（3）现从女生中抽取2人进一步调查，设其中喜爱打篮球的女生人数为
，求的分布列与期望.
下面的临界值表供参考：
 |
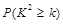0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式：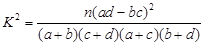
，其中
)
三棱锥P-ABC中，三侧棱PA、PB、PC两两相互垂直，三侧面面积分
别为S1、S2、S3，底面积为S，三侧面与底面分别成角α、β、γ，（1）求S（用S1、S2、S3表示）；（2）求证：cos2α+cos2β+cos2γ=1；
过点S引三条长度相等不共面的线段SA、SB、SC，且∠ASB=∠ASC=60°，
∠BSC=90°，求证：平面ABC⊥平面BSC。
如图，四棱锥V-ABCD中，∠BCD=∠BAD=90°，又∠BCV=∠BAV=90°，
求证：VD⊥AC；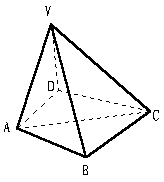
如图，正方体ABCD-A1B1C1D1的棱长为8cm，M、N、P分别是AB、A1D1、BB1的中点；（1）画出过M、N、P三点的平面与平面A1B1C1D1的交线以及与平面BB1C1C的交线；（2）设过M、N、P三点的平面与B1C1交于点Q，求PQ的长； 
在三棱锥A－BCD中,E、F分别是线段AD、BC上的点,满足
,AB=CD=3,且AB与CD所成的角为60o,求EF的长.