《列子》中《歧路亡羊》写道:
杨子之邻人亡羊,既率其党,又请杨子之竖追之。杨 子曰:“嘻!亡一羊,何追者之众?”邻人日:“多歧路。”既 反,问:“获羊乎?”日:“亡之矣。”曰:“奚亡之?”曰:“歧路 之中又有歧焉,吾不知所之,所以反也.”
如图,假定所有的分叉口都各有两条新的歧路,并且丢失的羊走每条歧路的可能性都相等.
(1)到第n次分歧时,共有多少条歧路?以当羊走过n个三叉路口后,找到羊的概率是多少?
(2)当n=5时,派出6个人去找羊,找到羊的概率是多少?
如图,在梯形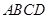 中,
中,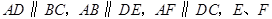 两点在边
两点在边 上,且四边形
上,且四边形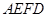 是平行四边形.
是平行四边形.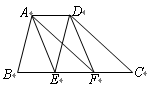
(1)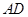 与
与 有何等量关系?请说明理由;
有何等量关系?请说明理由;
(2)当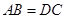 时,求证:
时,求证: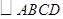 是矩形.
是矩形.
一辆汽车从A地驶往B地,前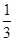 路段为普通公路,其余路段为高速公路.已知汽车在普通公路上行驶的速度为60km/h,在高速公路上行驶的速度为100km/h,汽车从A地到B地一共行驶了2.2h.
路段为普通公路,其余路段为高速公路.已知汽车在普通公路上行驶的速度为60km/h,在高速公路上行驶的速度为100km/h,汽车从A地到B地一共行驶了2.2h.
请你根据以上信息,就该汽车行驶的“路程”或“时间”,提出一个用二元一次方程组解决的问题,并写出解答过程.
一家医院某天出生了3个婴儿,假设生男生女的机会相同,那么这3个婴儿中,出现1个男婴、2个女婴的概率是多少?请用树状图说明。
某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下: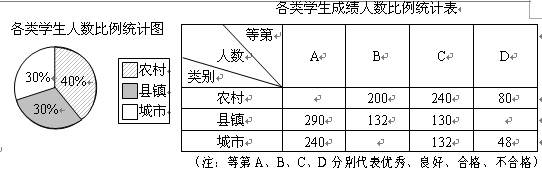
(1)请将上面表格中缺少的三个数据补充完整
(2)若该市九年级共有60 000名学生参加测试,试估计该市学生成绩合格以上(含合格)的人数.
如图所示,直线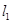 :
: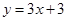 与
与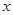 轴交于
轴交于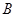 点,与直线
点,与直线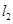 交于
交于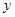 轴上一点
轴上一点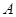 ,且
,且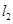 与
与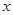 轴的交点为
轴的交点为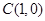 .
.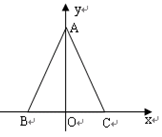
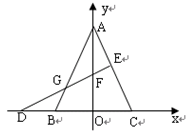
(1)求证: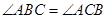 ;
;
(2)如图所示,过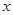 轴上一点
轴上一点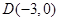 作
作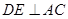 于
于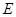 ,
,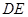 交
交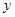 轴于
轴于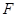 点,交
点,交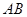 于
于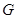 点,求
点,求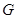 点的坐标.
点的坐标.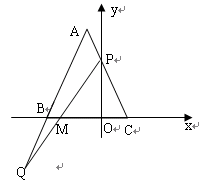
(3)如图所示,将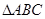 沿
沿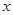 轴向左平移,
轴向左平移,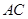 边与
边与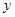 轴交于一点
轴交于一点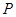 (
(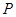 不同于
不同于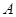 、
、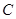 两点),过
两点),过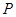 点作一直线与
点作一直线与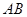 的延长线交于
的延长线交于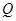 点,与
点,与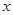 轴交于
轴交于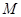 点,且
点,且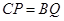 ,在
,在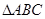 平移的过程中,线段
平移的过程中,线段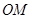 的长度是否发生变化?若不变,请求出它的长度;若变化,确定其变化范围.
的长度是否发生变化?若不变,请求出它的长度;若变化,确定其变化范围.