将一枚硬币抛起，使其自然下落，每抛两次作为一次实验，当硬币落定后，一面朝上，我们叫做“正”，另一面朝上，我们叫做“反”．
（1）一次实验中，硬币两次落地后可能出现几种情况图片来源，百度搜索→硬币．
（2）做20次实验，根据实验结果，填写下表．
| 结果 |
正正 |
正反 |
反反 |
| 频数 |
|
|
|
| 频率 |
|
|
|
（3）根据上表，制作相应的频数分布直方图．
（4）经观察，哪种情况发生的频率较大．
（5）实验结果为“正反”的频率是多大．
（6）5个同学结成一组，分别汇总其中两人，三人，四人，五人的实验数据，得到40次，60次，80次，100次的实验结果，将相应数据填入下表。
| 实验次数 |
40次 |
60次 |
80次 |
100次 |
| “正反”的频数 |
|
|
|
|
| “正反”的频率 |
|
|
|
|
（7）依上表，绘制相应的折线统计图．
（8）计算“正反”出现的概率．
（9）经过以上多次重复实验，所得结果为“正反”的频率与你计算的“正反”的概率是否相近．
某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下面是水平放置的破裂管道有水部分的截面．若这个输水管道有水部分的水面宽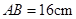
，水面最深地方的高度为4cm，求这个圆形截面的半径．
已知：如图，□ABCD中，BD是对角线，AE⊥BD于E，CF⊥BD于F.求证：BE=DF.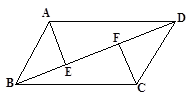
解不等式组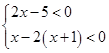
，并把解集在数轴上表示出来．
计算：
使得函数值为零的自变量的值称为函数的零点．例如，对于函数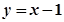
，令
，可得
，我们就说
是函数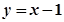的零点．请根据零点的定义解决下列问题：已知函数
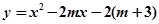（m为常数）．当m=0时，求该函数的零点
证明：无论m取何值，该函数总有两个零点；
设函数的两个零点分别为
和
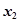，且
，此时函数图象与
轴的交点分别为A、B（点A在点B左侧），点M在直线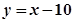
上，当MA+MB最小时，求直线AM的函数解析式．