20世纪60年代初期,科学家首先发现了“记忆金属”,“记忆金属”不同于一般的金属,它和有生命的生物一样,具有较强的“记忆性”,它能“记”住自己原来的形状.某人用一种记忆合金制成了太阳灶,为了便于储存和运输,在温度较低时将太阳灶压缩成了一个体积较小的球.使用时在太阳光的强烈照射下又恢复成了伞状.恢复形状后的太阳灶正对着太阳,它的半径为R.已知太阳的辐射功率(太阳每秒辐射的能量)为P,由于大气层的反射和吸收,太阳能只有1/a到达地面.若把太阳光看成是频率为ν的单色光,太阳中心到地面的距离为L,则这个太阳灶每秒钟能接收多少个光子?(普朗克常量为h)
在一次救援当中,为了救助伤员,直升机需要悬停在800 m的高空,用绳索将伤员从地面拉起,假设在某一次救助伤员时,悬绳以0.4 m/s2的加速度将静止于地面的伤员拉起,达到4 m/s的速度时,变为匀速上升,试求:
(1)伤员加速运动的时间和位移;
(2)伤员从地面到直升机需要多长时间.
(12分)一辆汽车以20m/s的速度在平直公路上行驶,现因故紧急刹车,已知汽车刹车过程中加速度的大小始终为5m/s2,求
(1)汽车刹车3s末的速度大小;
(2)汽车通过30m所需要的时间;
(3)汽车从开始刹车到6s末所通过的位移大小
(8分)猎豹是目前世界上陆地奔跑速度最快的动物,速度可达每小时110多公里,但不能维持长时间高速奔跑,否则会因身体过热而危及生命.猎豹在一次追击猎物时可认为做匀加速直线运动经4s速度由静止达到最大,然后匀速运动保持了4s仍没追上猎物,为保护自己它放弃了这次行动,以大小3m/s2的加速度做匀减速运动,经10s停下,设猎豹此次追捕始终沿直线运动。
求:(1)猎豹奔跑的最大速度可达多少?
(2)猎豹加速时的加速度多大?
(13分)如图甲所示,场强大小为E、方向竖直向上的匀强电场内存在着一半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最低点,B点是圆形区域最右侧的点。在A点有放射源释放出初速度大小不同、方向均垂直于场强向右的正电荷,电荷的质量均为m,电量均为q,不计重力。试求:
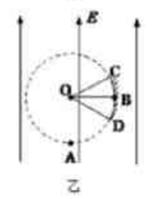
(1)电荷在电场中运动的加速度多大?
(2)运动轨迹经过B点的电荷在A点时的速度多大?
(3)若在圆形区域的边缘有一圆弧形接收屏CBD,B点仍是圆形区域最右侧的点,C、D分别为接收屏上最边缘的两点,如图乙所示,∠COB=∠BOD=37°。求该屏上接收到的电荷的末动能大小的范围。(提示:sin37°=0.6,cos37°=0.8。)
(12分)如图所示电路中,电源电动势E=10V,内阻 r= 0.5Ω,电动机的电阻R0 =
1.0Ω,电阻R1=1.5Ω。电动机正常工作时,电压表的示数U1=3.0V,求:
(1)电源总功率?
(2)电动机消耗的电功率?
(3)电源的输出功率?