有20箱橘子,以每箱25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
| 与标准质量的差值 (单位:千克) |
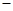 3 3 |
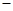 2 2 |
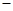 1.5 1.5 |
0 |
1 |
2.5 |
| 箱数 |
1 |
4 |
2 |
3 |
2 |
8 |
(1)20箱橘子中,最重的一箱比最轻的一箱多重多少千克?
(2)与标准重量比较,20箱橘子总计超过或不足多少千克?
(3)若橘子每千克售价2.6元,则出售这20箱橘子可卖多少元?(结果保留整数)
如图所示,一个大正方形的面上,编号为1,2,3,4的地块,是四个全等的等腰直角三角形空地,中间是小正方形绿色草坪,一名训练有素的跳伞运动员,每次跳伞都能落在大正方形地面上.
(1)求跳伞运动员一次跳伞落在草坪上的概率;
(2)求跳伞运动员两次跳伞都落在草坪上的概率.
田忌赛马的故事为我们熟知.小亮与小齐学习概率初步知识后设计了如下游戏:小亮手中有方块10、8、6三张扑克牌,小齐手中有方块9、7、5三张扑克牌.每人从各自手中取出一张牌进行比较,数字大的为本“局”获胜,每次取得牌不能放回.
(1)若每人随机取手中的一张牌进行比赛,求小齐本“局”获胜的概率;
(2)若比赛采用三局两胜制,即胜2局或3局者为本次比赛获胜者.当小亮的三张牌出牌顺序为先出6,再出8,最后出10时,小齐随机出牌应对,求小齐本次比赛获胜的概率.
如图,4张背面完全相同的纸牌(用①、②、③、④表示),在纸牌的正面分别写有四个不同的条件,小明将这4张纸牌背面朝上洗匀后,先随机摸出一张(不放回),再随机摸出一张.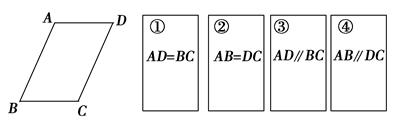
(1)用树状图(或列表法)表示两次摸牌出现的所有可能结果;
(2)以两次摸出牌上的结果为条件,求能判断四边形ABCD是平行四边形的概率.
某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款人数的比为1∶5.
捐款人数分组统计表
| 组别 |
捐款额x/元 |
人数 |
| A |
1≤x<10 |
a |
| B |
10≤x<20 |
100 |
| C |
20≤x<30 |
|
| D |
30≤x<40 |
|
| E |
x≥40 |
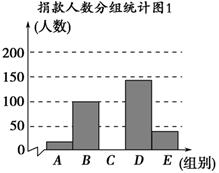
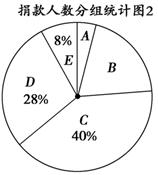
请结合以上信息解答下列问题.
(1)a=________,本次调查样本的容量是________;
(2)先求出C组的人数,再补全“捐款人数分组统计图1”;
(3)若任意抽出1名学生进行调查,恰好是捐款数不少于30元的概率是多少?
据衢州市2011年国民经济和社会发展统计公报显示,2011年衢州市新开工的住房有商品房、廉租房、经济适用房和公共租赁房四种类型.老王对这四种新开工的住房套数和比例进行了统计,并将统计结果绘制成下面两幅统计图,请你结合图中所给信息解答下列问题: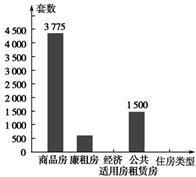

(1)求经济适用房的套数,并补全频数分布直方图;
(2)假如申请购买经济适用房的对象中共有950人符合购买条件,老王是其中之一.由于购买人数超过房子套数,购买者必须通过电脑摇号产生.如果对2011年新开工的经济适用房进行电脑摇号,那么老王被摇中的概率是多少?
(3)如果2012年新开工廉租房建设的套数比2011年增长10%,那么2012年新开工廉租房有多少套?