在平面直角坐标系xoy中， 一块含60°角的三角板作如图摆放，斜边 AB在x轴上，直角顶点C在y轴正半轴上，已知点A（－1，0）．
（1）请直接写出点B、C的坐标：B（ ， ）、C（ ， ）；并求经过A、B、C三点的抛物
线解析式；
（2）现有与上述三角板完全一样的三角板DEF（其中∠EDF=90°，∠DEF=60°），把顶点E放在线段
AB上（点E是不与A、B两点重合的动点），并使ED所在直线经过点C． 此时，EF所在直线与（1）中的抛物线交于第一象限的点M．
①设AE=x，当x为何值时，△OCE∽△OBC；
②在①的条件下探究：抛物线的对称轴上是否存在点P使△PEM是等腰三角形，若存在，请求点P的坐标；若不存在，请说明理由．
(1) 请你在数轴上表示下列有理数：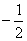
，
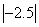，0，－22，－(－4)．
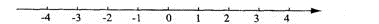
(2) 将上列各数用“＜”号连接起来：_______________________．
下面是按一定规律排列的一列数：
第1个数：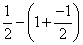
；
第2个数：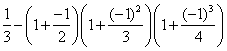
；
第3个数：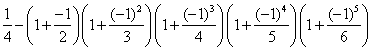
；
……
第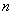
个数：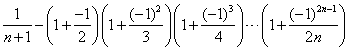
．
那么，在第10个数、第11个数、第12个数、第13个数中，最大的数是（ ）
| A．第10个数 | B．第11个数 | C．第12个数 | D．第13个数 |
3．已知：a为有理数，a3+a2+a+1=0，求1+a+a2+a3+…+a2012的值．
4．已知：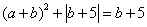
，
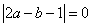，求ab的值。
5．当整数k为何值时，方程9x-3=kx+14有正整数解？并求出正整数解
若a, b之间有9个整数（不含a, b本身），则a—b的范围是____
（1）填空：1—2+3—4+……+49—50=_____________；
1—2+3—4+……+99—100+101=_____________；
（2）计算：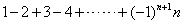
如图所示，用三种大小不同的六个正方形和一个缺角的正方形拼成长方形ABCD,其中，GH="2cm," GK="2cm," 设BF="x" cm,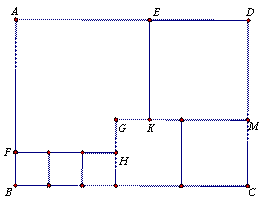
（1）用含x的代数式表示CM=_____________cm，DM=_____________cm.
（2）若DC=10cm，求x的值.
（3）求长方形ABCD的面积.