下表为某照相馆的价目表,今逢开业周年庆,底片冲洗与照片冲洗皆打八折,小颖带了一卷底片去冲洗相纸为“布纹”的照片若干张,打折后共付了16.8元.请问小颖洗了多少张照片?
| 项 目 |
费 用 |
| 底片冲洗费 |
3元/卷 |
| 相纸规格(布纹)照片扩展费 |
0.50元/张 |
解不等式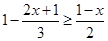 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.
如图,点A,B,D,E在同一直线上,AB=ED,AC∥EF,∠C=∠F.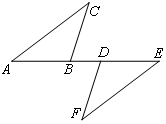
求证:AC=EF.
(本题12分)某商场用18万元购进A、B两种商品,其进价和售价如下表:
| A |
B |
|
| 进价(元/件) |
1200 |
1000 |
| 售价(元/件) |
1380 |
1200 |
(1)若销售完后共获利3万元,该商场购进A、B两种商品各多少件;
(2)若购进B种商品的件数不少于A种商品的件数的6倍,且每种商品都必须购进.
① 问共有几种进货方案?
② 要保证利润最高,你选择哪种进货方案?
(本题10分)如图,直线AB和直线CD、直线BE和直线CF都被直线BC所截.在下面三个式子中,请你选择其中两个作为条件,剩下的一个作为结论,组成一个真命题并证明.
①AB⊥BC、CD⊥BC,②BE∥CF,③∠1=∠2.
条件(已知):
结论(求证):
证明: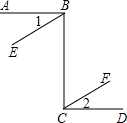
(本题10分)若不等式组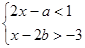 的解集是
的解集是 ,
,
(1)求代数式 的值;
的值;
(2)若 ,
,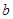 ,
,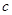 为某三角形的三边长,试求
为某三角形的三边长,试求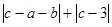 的值.
的值.