已知函数f(x)=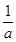 -
-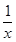 (a>0,x>0).
(a>0,x>0).
(1)用函数的单调性定义证明:f(x)在(0,+∞)上是增函数;
(2)若f(x)在[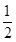 ,2]上的值域是[
,2]上的值域是[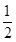 ,2],求实数a的值.
,2],求实数a的值.
(本小题满分12分)已知圆 经过
经过 、
、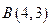 两点,且圆心在直线
两点,且圆心在直线 上.
上.
(1)求圆 的方程;
的方程;
(2)若直线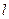 经过点
经过点 且与圆
且与圆 相切,求直线
相切,求直线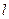 的方程.
的方程.
(本小题满分12分)
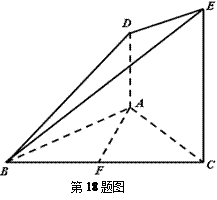
如图所示,凸多面体 中,
中,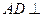 平面
平面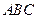 ,
,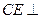 平面
平面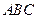 ,
, ,
,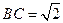 ,
,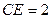 ,
,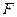 为
为 的中点.
的中点.
(1)求证: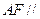 平面
平面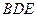 ;
;
(2)求证:平面 平面
平面 .
.
(本小题满分12分)袋中有大小、形状相同的红、黑球各一个,现有放回地随机摸3次,每次摸取一个球,考虑摸出球的颜色。
(1)试写出此事件的基本事件空间;
(2)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分不小于5分的概率。
(本 小题满分10分)选修4-5:不等式选讲
小题满分10分)选修4-5:不等式选讲
设函数
(I)若a=-1,解不等式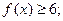
(II)如果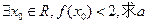 的取值范围。
的取值范围。
请考生在22、23两题中任选一题作答,如果都做,则按所做的第一题记分。
(本小题满分10分)选修4-1:几何证明选讲
如图,AB是⊙O的直径,C、F为⊙O上的点,CA是∠BAF的角平分线,过点C
作CD⊥AF交AF的延长线于D点,CM⊥AB,垂足为点M。
(I)求证:DC是⊙O的切线; (II)求证:AM:MB= DF·DA。
DF·DA。