已知函数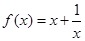 .
.
(1)判断函数的奇偶性,并加以证明;
(2)用定义证明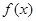 在
在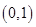 上是减函数;
上是减函数;
(3)函数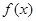 在
在 上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
(高考真题)一款击鼓小游戏的规则如下:每盘游戏都需要击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得 分,出现两次音乐获得
分,出现两次音乐获得 分,出现三次音乐获得
分,出现三次音乐获得 分,没有出现音乐则扣除
分,没有出现音乐则扣除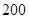 分(即获得
分(即获得 分)。设每次击鼓出现音乐的概率为
分)。设每次击鼓出现音乐的概率为 ,且各次击鼓出现音乐相互独立。
,且各次击鼓出现音乐相互独立。
(Ⅰ)设每盘游戏获得的分数为 ,求
,求 的分布列;
的分布列;
(Ⅱ)玩三盘游戏,至少有一盘出现音乐的概率是多少?
(Ⅲ)玩这款游戏的许多人都发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了。请运用概率统计的相关知识分析分数减少的原因。
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品作为样本称出它们的重量(单位:克),重量的分组区间为(490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图所示.
(1)根据频率分布直方图,求重量超过505克的产品数量;
(2)在上述抽取的40件产品中任取2件,设Y为重量超过505克的产品数量,求Y的分布列;
(3)从该流水线上任取5件产品,求恰有2件产品的重量超过505克的概率.
下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.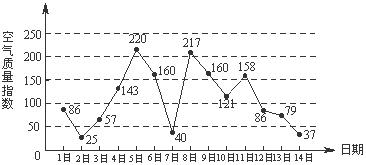
(Ⅰ)求此人到达当日空气重度污染的概率;
(Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
随机变量X的分布列为
| X |
1 |
2 |
4 |
| P |
0.4 |
0.3 |
0.3 |
则E(5X+4)等于()
A.15 B.11 C.2.2 D.2.3
箱子里有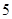 个黑球,
个黑球, 个白球,每次随机取出一个球,若取出黑球,则放回箱中,重新取球;若取出白球,则停止取球,那么在第
个白球,每次随机取出一个球,若取出黑球,则放回箱中,重新取球;若取出白球,则停止取球,那么在第 次取球之后停止的概率为
次取球之后停止的概率为
A. |
B. |
C. |
D. |