在如图的方格纸中(每个小方格的边长都是1个单位)有一点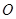 和
和 .
.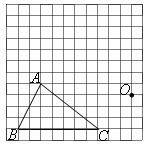
(1)请以点 为位似中心,把
为位似中心,把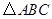 缩小为原来的一半(不改变方向),得到
缩小为原来的一半(不改变方向),得到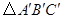 .
.
(2)请用适当的方式描述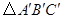 的顶点
的顶点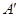 ,
,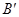 ,
,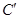 的位置.
的位置.
矩形纸片ABCD的长AD为4cm,宽AB为3cm,把矩形纸片拼叠,使相对两顶点A,C重合,然后展开,求折痕EF的长.
如图①所示,在正方形ABCD中,M是AB的中点,E是AB的延长线上一点,MN⊥DM,且交∠CBE的平分线于点N.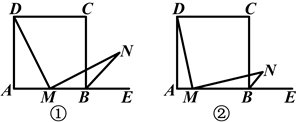
(1)求证:MD=MN;
(2)若将上述条件中“M是AB的中点”改成“M是AB上任意一点”,其余条件不变,如图②所示,则结论“MD=MN”还成立吗?若成立,给出证明;若不成立,请说明理由.
如图所示,□ABCD中,对角线AC,BD相交于点O,过点O作直线交AD于点E,交BC于点F,若□ABCD的面积为30cm2,求阴影部分的面积.
如图是边长为30cm的菱形衣帽架,若∠1=60°,则AB、AC的长各是多少?
如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
(1)求证:CD=AN;
(2)若∠AMD=2∠MCD,求证:四边形ADCN是矩形.