射击集训队在一个月的集训中,对甲、乙两名运动员进行了10次测试,成绩如图所示(折线图中,粗线表示甲,细线表示乙):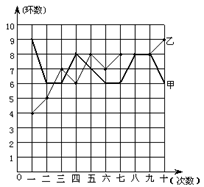
⑴根据图中所提供的信息填写下表:
⑵如果你是教练,会选择哪位运动员参加比赛?请结合上表中三个统计指标以及折线统计图说明理由。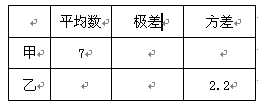
雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;
(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?
如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:
| 朝下数字 |
1 |
2 |
3 |
4 |
| 出现的次数 |
16 |
20 |
14 |
10 |
(1)计算上述试验中“4朝下”的频率是__________;
(2)随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于4的概率
如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
(1)把△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
(本题每小题8分,共16分)
(1)(x+1)2=2
(2)x2-2x-3="0" (用适当的方法)
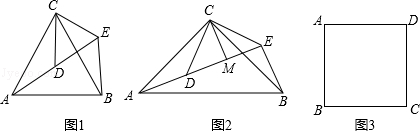
(1)如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
①∠AEB的度数为;
②线段AD,BE之间的数量关系为;
(2)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由;
(3)如图3,在正方形ABCD中,CD= ,若点P满足PD=1,且∠BPD=90°,请求出点A到BP的距离.
,若点P满足PD=1,且∠BPD=90°,请求出点A到BP的距离.