（1）如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．
①∠AEB的度数为 ；
②线段AD，BE之间的数量关系为 ；
（2）如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由；
（3）如图3，在正方形ABCD中，CD=
，若点P满足PD=1，且∠BPD=90°，请求出点A到BP的距离．
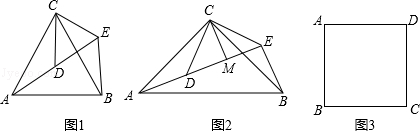
李明在计算一个多项式减去
时，误认为加上此式，计算出错误结果为
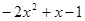，请求出正确答案。
为何值时，-3是关于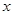
的一元一次方程：
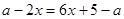的解。
解方程：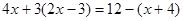
在平面直角坐标系中，抛物线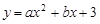
与
轴的两个交点分别为A（-3，0）、B（1，0），过顶点C作CH⊥x轴于点H.
（1）求抛物线的解析式和顶点坐标；
（2）在
轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标. 
如图，四边形ABCD中，AD＝CD，∠DAB＝∠ACB＝90°，过点D作DE⊥AC，垂足为F，DE与AB相交于点E．
（1）求证：AB·AF＝CB·CD；
（2）已知AB＝15 cm，BC＝9 cm，P是射线DE上的动点．设DP＝x cm（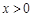
），四边形BCDP的面积为y cm2．
①求y关于x的函数关系式；
②当x为何值时，△PBC的周长最小，并求出此时y的值．