金银花自古被誉为清热解毒的良药，同时也是很多高级饮料的常用原料．“渝蕾一号”为重庆市中药研究院所选育的金银花优良品种，较传统金银花具有质量好、产量高、结蕾整齐等优点．某花农于前年引进一批“渝蕾一号”金银花种苗进行种植，去年第一次收获．因金银花入药或作饮料需要使用干燥花蕾，该花农将收获的新鲜金银花全部干燥成干花蕾后出售．根据经验，每亩鲜花蕾产量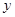
（千克）与每亩种苗数
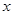（株）满足关系式：
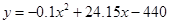，每亩成本
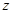（元）与每亩种苗数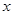（株）之间的函数关系满足下表：
（1）请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，求出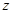与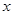的函数关系式；
（2）若该品种金银花的折干率为20%（即每100千克鲜花蕾，干燥后可得20千克干花蕾），去年每千克干花蕾售价为200元，则当每亩种苗数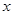为多少时，每亩销售利润
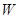可获得最大值，并求出该最大利润；（利润=收入
成本）
（3）若该花农按照（2）中获得最大利润的方案种植，并不断改善养植技术，今年每亩鲜花蕾产量比去年增加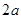
%．但由于市场上同类产品数量猛增，造成每千克干花蕾的售价比去年降低
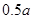%，结果今年每亩销售总额为45810元．请你参考以下数据，估算出
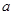的整数值（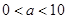
）．
（参考数据：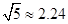
，
，
，
）
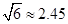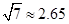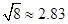解方程（每小题4分，共16分）
（1）
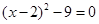
（2）
（3）
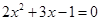
（4）
己知：二次函数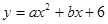
与x轴交于A、B两点（点A在点B的左侧），点A、点B的横坐标分别为一元二次方程
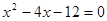的两个根．
（1）求出该二次函数表达式及顶点坐标；
（2）如图1，在抛物线对称轴上是否存在点P，使△APC的周长最小，若存在，请求出点P的坐标：若不存在，请说明理由；
（3）如图2，连接AC、BC，点Q是线段OB上一个动点（点Q不与点O、B重合）．过点Q作QD∥AC交BC于点D，设Q点坐标（m，0），当△CDQ面积S最大时，求m的值．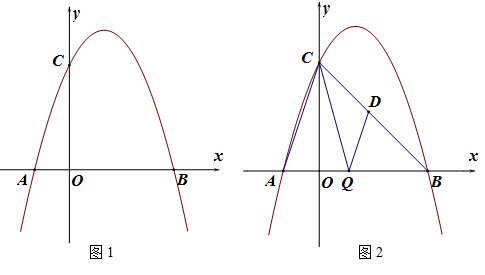 
已知：关于x的函数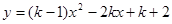
的图象与x轴有交点．
（1）求k的取值范围；
（2）若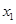
，
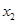是函数图象与x轴两个交点的横坐标，且满足
．
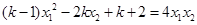①求k的值；②当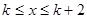
时，求函数y的最大值和最小值．
小丽为校合唱队购买某种服装时，商店经理给出了如下优惠条件：如果一次性购买不超过10件，单价为80元：如果一次性购买多于10件，那么每增加1件，购买的所有服装的单价降低2元，但单价不得低于50元．按此优惠条件，小丽一次性购买了这种服装x件．
（1）当x= 时，小丽购买的这种服装的单价为76元；
（2）小丽一次性购买这种服装付了1200元．请问她购买了多少件这种服装？
某校为了开阔学生的视野，积极组织学生参加课外读书活动．“放飞梦想”读书小组协助老师随机抽取本校的部分学生，调查他们最喜爱的图书类别（图书分为文学类、艺体类、科普类、其他等四类），并将调查结果绘制成如下两幅不完整的统计图，请你结合图中的信息解答下列问题：
（1）求被调查的学生人数；
（2）补全条形统计图；
（3）已知该校有1200名学生，估计全校最喜爱文学类图书的学生有多少人？