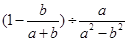己知:二次函数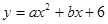 与x轴交于A、B两点(点A在点B的左侧),点A、点B的横坐标分别为一元二次方程
与x轴交于A、B两点(点A在点B的左侧),点A、点B的横坐标分别为一元二次方程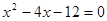 的两个根.
的两个根.
(1)求出该二次函数表达式及顶点坐标;
(2)如图1,在抛物线对称轴上是否存在点P,使△APC的周长最小,若存在,请求出点P的坐标:若不存在,请说明理由;
(3)如图2,连接AC、BC,点Q是线段OB上一个动点(点Q不与点O、B重合).过点Q作QD∥AC交BC于点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值. 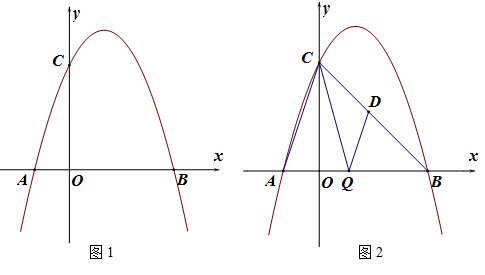
如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.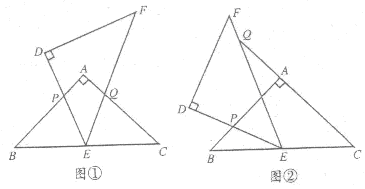
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=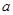 ,CQ=
,CQ= 时,P、Q两点间的距离 (用含
时,P、Q两点间的距离 (用含 的代数式表示).
的代数式表示).
某校将举办“心怀感恩·孝敬父母”的活动,为此,校学生会就全校1 000名同学暑假期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成如下条形统计图.
(1)本次调查抽取的人数为_______,估计全校同学在暑假期间平均每天做家务活的时间在40分钟以上(含40分钟)的人数为_______;
(2)校学生会拟在表现突出的甲、乙、丙、丁四名同学中,随机抽取两名同学向全校汇报.请用树状图或列表法表示出所有可能的结果,并求恰好抽到甲、乙两名同学的概率.
如图,一次函数 (
( 为常数)的图象与反比例函数
为常数)的图象与反比例函数 (
( 为常数,且
为常数,且 ≠0)的图象交于A,B两点,且点A的坐标为(
≠0)的图象交于A,B两点,且点A的坐标为( ,4).
,4).
(1)分别求出反比例函数及一次函数的表达式;
(2)求点B的坐标.
如图,在一次测量活动中,小华站在离旗杆底部(B处)6米的D处,仰望旗杆顶端A,测得仰角为60°,眼睛离地面的距离ED为1.5米.试帮助小华求出旗杆AB的高度.(结果精确到0.1米,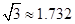 )
)
化简: