如图①所示,已知A、B为直线l上两点,点C为直线l上方一动点,连接AC、BC,分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1⊥l于点D1,过点E作EE1⊥l于点E1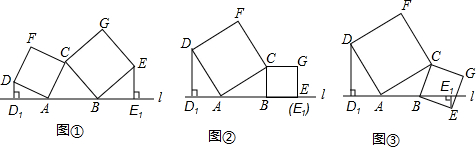
(1)如图②,当点E恰好在直线l上时(此时E1与E重合),试说明DD1=AB;
(2)在图①中,当D、E两点都在直线l的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,并说明理由;
(3)如图③,当点E在直线l的下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系.(不需要证明)
如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O于D,AD的延长线交BC于E,若∠C = 25°,求∠A的度数.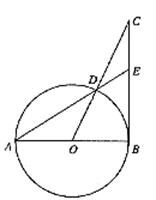
解一元二次方程:(1)(x+1)2="3"
(2)3y2+4y+1=0
(本题满分8 分)化简二次根式:
分)化简二次根式:(1)
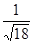
(2)
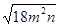 (
( <0)
<0)
(本题12分) 如图,已知二次函数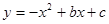 的图象与
的图象与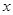 轴交于点
轴交于点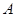 、
、 ,与
,与 轴交于点
轴交于点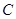 ,其顶点为
,其顶点为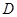 ,且直线
,且直线 的解析式为
的解析式为 .
.(1) 求二次函数的解析式.
(2) 求△ABC外接圆的半径及外心的坐标;
(3) 若点P是第一象限内抛物线上一动点,求四边形ACPB的面积最大值.

(本题12分) 在正方形网格中,A、B为格点,以点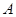 为圆心,
为圆心,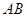 为半径作圆
为半径作圆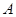 交网格线于点
交网格线于点 (如图(1)),过点
(如图(1)),过点 作圆的切线交网格线于点
作圆的切线交网格线于点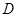 ,以点
,以点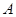 为圆心,
为圆心,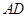 为半径作圆交网格线于点
为半径作圆交网格线于点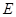 (如图(2)).
(如图(2)).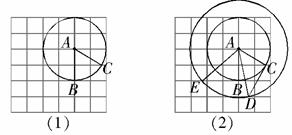
问题:(1) 求
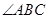 的度数;
的度数;(2) 求证:
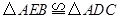 ;
;(3)
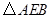 可以看作是由
可以看作是由 经过怎样的变换得到的?并判断
经过怎样的变换得到的?并判断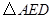 的形状(不用说明理由).
的形状(不用说明理由).(4) 如图(3),已知直线
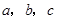 ,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形
,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形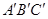 ,使三个顶点
,使三个顶点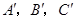 ,分别在直线
,分别在直线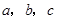 上.要求写出简要的画图过程,不需要说明理由.
上.要求写出简要的画图过程,不需要说明理由.