某市从今年元月1日起调整居民用水价格,每立方米水费上涨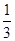 ,小丽家去年12月的水费是15元,而今年7月份的水费则是30元,已知小丽家今年7月的用水量比去年12月份的用水量多5立方米,求该市今年居民用水的价格.
,小丽家去年12月的水费是15元,而今年7月份的水费则是30元,已知小丽家今年7月的用水量比去年12月份的用水量多5立方米,求该市今年居民用水的价格.
A、B两地相距100公里,甲骑电瓶车由A往B出发,1小时30分钟后,乙开着小汽车也由A往B.已知乙的车速为甲的车速的2.5倍,且乙比甲提前1小时到达,求两人的速度各是多少?
一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,求江水的流速为多少?
某单位将沿街的一部分房屋出租作为店面房,每间房屋的租金第二年比第一年多500元,所有房屋出租的租金第一年为9.6万元,第二年为10.2万元.
(1)求出租的房屋总间数;
(2)分别求历年每间房屋的租金.
某商场销售某种商品,第一个月将此商品的进价提高 作为销售价,共获利
作为销售价,共获利 元.第二个月商场搞促销活动,将商品的进价提高
元.第二个月商场搞促销活动,将商品的进价提高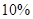 作为销售价,第二个月的销售量比第一个月增加了
作为销售价,第二个月的销售量比第一个月增加了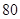 件,并且商场第二个月比第一个月多获利
件,并且商场第二个月比第一个月多获利 元.问此商品的进价是多少元?商场第二个月共销售多少件?
元.问此商品的进价是多少元?商场第二个月共销售多少件?