某同学根据自己的生活体验设置了这样一个问题:甲物体沿直线MN做匀速直线运动,速度为v1. P点到MN的垂直距离为s,如图所示. 乙物体由P点开始运动,要追上甲物体. 设乙物体可沿任意方向运动且速度大小始终是v2. 已知v2>v1. 某时刻当甲位于直线MN上的F点时,乙物体由P点开始运动,问,乙物体能否追上甲物体?哪种追赶方式用时最短?同学们通过分析以后得出以下几种不同的观点,你认为正确的是( )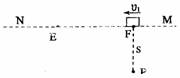
| A.乙物体沿PFN的路线追赶甲物体时,用时最短 |
| B.乙物体追赶过程中,保持其速度的方向总是指向甲物体,这样运动方式用时最短 |
| C.通过计算,使乙物体沿某直线PE运动,到达直线MN时正好与甲物体相遇,这种方式用时最短 |
| D.在A、B、C三种追赶方式中,乙物体都能追上甲物体 |
一线城市道路越来越拥挤,因此自行车越来越受城市人们的喜爱,如图,当你骑自行车以较大的速度冲上斜坡时,假如你没有蹬车,受阻力作用,则在这个过程中,下面关于你和自行车的有关说法正确的是()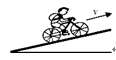
| A.机械能减少 |
| B.克服阻力做的功等于机械能的减少量 |
| C.减少的动能等于增加的重力势能 |
| D.因为要克服阻力做功,故克服重力做的功小于重力势能的增加量 |
宇航员在某星球表面完成下面实验:如图所示,在半径为r的竖直光滑圆弧轨道内部,有一质量为m的小球(可视为质点),在最低点给小球某一水平初速度,使小球在竖直面内做圆周运动,测得轨道在最高点和最低点时所受压力大小分别为F1、F2;已知该星球的半径为R,引力常量G,则该星球的第一宇宙速度是()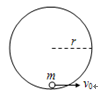
A.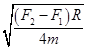 |
B.  |
C.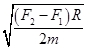 |
D.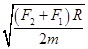 |
如图所示为四分之一圆柱体OAB的竖直截面,半径为R,在B点上方的C点水平抛出一个小球,小球轨迹恰好在D点与圆柱体相切,OD与OB的夹角为60°,则C点到B点的距离为()
A.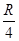 |
B.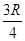 |
C.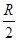 |
D.R |
如图甲、乙所示,倾角为θ的斜面上放置一滑块M,在滑块M上放置一个质量为m的物块,M和m相对静止,一起沿斜面匀速下滑,下列说法正确的是()
| A.图甲中物块m受到摩擦力,方向水平向左 |
| B.图乙中物块m受到摩擦力,方向与斜面平行向上 |
| C.图甲中物块M受到5个力 |
| D.图乙中物块M受到6个力 |
a、b两物体从同一位置沿同一直线运动,它们的v-t图象如图所示,下列说法正确的是()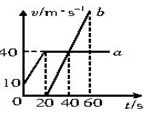
| A.a、b加速时,物体a的加速度大于物体b的加速度 |
| B.20s时,a、b两物体相距最远 |
| C.60s时,物体a在物体b的前方 |
| D.40s时,a、b两物体的速度相等,相距200m |