在一个半径为R0的星球表面上,宇航员做了一个平抛实验:将一个小球以初速度v0水平抛出,经过时间t0,小球恰好垂直打在一个倾角为θ的斜坡上.已知万有引力常量为G,请用以上物理量表示出该星球的平均密度.(星球可看作球体)
地面上有一个半径为R的圆形跑道,高为h的平台边缘上的P点在地面上P′点的正上方,P′与跑道圆心O的距离为L(L>R),如图所示。跑道上停有一辆小车,现从P点水平抛出小沙袋,使其落入小车中(沙袋所受空气阻力不计)。问:
(1)若小车在跑道上运动,则沙袋被抛出时的初速度在什么范围内?
(2)若小车沿跑道顺时针做匀速圆周运动,当小车恰好经过A点时,将沙袋抛出,为使沙袋能在B处落入小车中,小车的速率v应满足什么条件?
汽车发动机的额定功率P0=150kW,汽车的质量m=5.0×103㎏,汽车在水平路面上行驶驶时,阻力是车重的k=0.10倍,重力加速度g=10m/s2.(所有计算结果保留两位有效数字)
(1)若汽车保持额定功率不变从静止启动,当车速为v1=10m/s时其加速度a1是多大?
(2)若汽车从静止开始,保持以a="1.0" m/s2的加速度做匀加速直线运动,维持这一过程的时间t是多长?这一过程中汽车牵引力做功W是多少?
已知地球同步卫星离地面的高度约为地球半径的6倍,若某行星的平均密度为地球平均密度的一半,它的同步卫星距其表面的高度是其半径的2.5倍,则该行星的的自转周期为多少小时?
用竖直向上大小为30 N的力F,将质量为2 kg的物体从地面由静止提升,物体上升2m后撤去力F,经一段时间后,物体落回地面。若忽略空气阻力,g取10 m/s2。求:
(1)拉力F做的功
(2)物体上升2m时的动能
(3)物体刚落回地面时的速度
如图,质量为m1=1kg,m2=4.5kg的两个小滑块固定在轻质弹簧两端,静止于光滑水平面上,m1靠在光滑竖直墙上。现在一质量为m=0.5kg的小滑块,以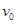 =12m/s,极短时间内撞上m2并粘在一起,最后m1与m2、m都将向右运动。在这个过程中,竖直墙对m1的冲量。
=12m/s,极短时间内撞上m2并粘在一起,最后m1与m2、m都将向右运动。在这个过程中,竖直墙对m1的冲量。