如图所示，光滑水平直轨道上放置长木板B和滑块C，滑块A置于B的左端，且A、B间接触面粗糙，三者质量分别为mA =" 1" kg 、mB =" 2" kg、 mC =" 23" kg ．开始时 A、B一起以速度v0 ="10" m/s向右运动，与静止的C发生碰撞，碰后C向右运动，又与竖直固定挡板碰撞，并以碰前速率弹回，此后B与C不再发生碰撞．已知B足够长，A、B、C最终速度相等．求B与C碰后瞬间B的速度大小．
在光滑的水平面上，质量为m1的小球A以速率v0向右运动．在小球A的前方O点有一质量为m2的小球B处于静止状态，如图所示．小球A与小球B发生正碰后小球A、B均向右运动．小球B被在Q点处的墙壁弹回后与小球A在P点相遇，PQ＝1.5PO.假设小球间的碰撞及小球与墙壁之间的碰撞都是弹性的，求两小球碰撞后的速度大小之比及质量之比m1∶m2. 
雅安地震时，震源同时产生了两种波，一种是传播速度约为3.5km/s的S波，另一种是传播速度约为7.0km/s的P波．地震发生时，雅安地震监测点记录到首次到达的P波比首次到达的S波早3min．假定地震波沿直线传播，震源的振动周期为1.2s，求震源与雅安监测点之间的距离x和S波的波长
如图所示为一均匀薄壁U形管，左管上端封闭，右管开口且足够长，管的横截面积为S=1×10-4 m2,内装水银，右管内有一质量为m="0.1" kg的活塞搁在固定卡口上，卡口比左管上端高出L="20" cm，活塞与管壁间非常密封且无摩擦，右管内封闭有一定质量的气体.起初温度为t0="27" ℃时，左、右管内液面高度相等，且左管内充满水银，右管内封闭气体的压强为p1=p0=1.0×105 Pa="75" cmHg.现使右管内气体温度逐渐升高,求：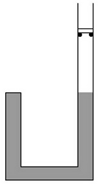
①温度升高到多少K时，右管活塞开始离开卡口上升？
②温度升高到多少K时，活塞上升到离卡口4 cm处？
如图所示，物体A的质量M=1kg，静止在光滑水平面上的平板车B的质量为m=0.5kg、长为L=1m．某时刻物体A以v0=4m/s向右的初速度滑上木板B的上表面，在A滑上B的同时，给B施加一个水平向右的拉力F=5N．忽略物体A的大小，已知A与B之间的动摩擦因数μ=0.2，重力加速度取g=10m/s2，试求：
（1）物体A在平板车上经多长时间与平板车有相同的速度；
（2）物体A在小车上运动时相对小车向右滑行的最大距离．
（3）如果要使A不至于从B上滑落，拉力F大小应满足的条件．
（本题12分）如图所示，一质量为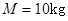
，长为
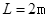的木板放在水平地面上，已知木板与地面间的动摩擦因数为
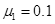，在此木板的右端上还有一质量为
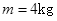的小物块，且视小物块为质点，木板厚度不计．今对木板突然施加一个
的水平向右的拉力，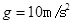
．
（1）若木板上表面光滑，则小物块经多长时间将离开木板？
（2）若小物块与木板间的动摩擦因数为
、小物块与地面间的动摩擦因数为
，小物块相对木板滑动一段时间后离开继续在地面上滑行，且对地面的总位移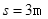
时停止滑行，求值．