如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD=BD=a,E是CC1的中点,A1D⊥BE.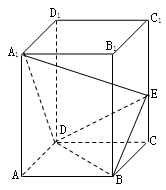
(I)求证:A1D⊥平面BDE;
(II)求二面角B―DE―C的大小;
(III)求点B到平面A1DE的距离
已知ΔABC中,满足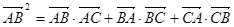 ,a,b,c分别是ΔABC的三边。
,a,b,c分别是ΔABC的三边。
(1)试判定ΔABC的形状,并求sinA+sinB的取值范围。
(2)若不等式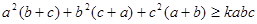 对任意的a,b,c都成立,求实数k的取值范围。
对任意的a,b,c都成立,求实数k的取值范围。
如图,圆 与离心率为
与离心率为 的椭圆
的椭圆 (
( )相切于点
)相切于点 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点 引两条互相垂直的两直线
引两条互相垂直的两直线 、
、 与两曲线分别交于点
与两曲线分别交于点 、
、 与点
与点 、
、 (均不重合).
(均不重合).
(ⅰ)若 为椭圆上任一点,记点
为椭圆上任一点,记点 到两直线的距离分别为
到两直线的距离分别为 、
、 ,求
,求 的最大值;
的最大值;
(ⅱ)若 ,求
,求 与
与 的方程.
的方程.
已知函数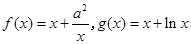 ,其中
,其中 .
.
(Ⅰ)若 是函数
是函数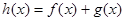 的极值点,求实数
的极值点,求实数 的值;
的值;
(Ⅱ)若对任意的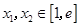 (
(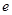 为自然对数的底数)都有
为自然对数的底数)都有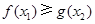 成立,求实数
成立,求实数 的取值范围.
的取值范围.
设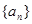 是各项都为正数的等比数列,
是各项都为正数的等比数列, 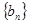 是等差数列,且
是等差数列,且 ,
,

(Ⅰ)求数列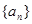 ,
,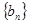 的通项公式;
的通项公式;
(Ⅱ)设数列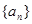 的前
的前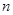 项和为
项和为 ,求数列
,求数列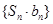 的前
的前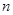 项和
项和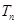 .
.
四名教师被分到甲、乙、丙三所学校参加工作,每所学校至少一名教师.
(Ⅰ)求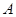 、
、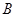 两名教师被同时分配到甲学校的概率;
两名教师被同时分配到甲学校的概率;
(Ⅱ)求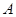 、
、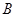 两名教师不在同一学校的概率;
两名教师不在同一学校的概率;
(Ⅲ)设随机变量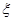 为这四名教师中分配到甲学校的人数,求
为这四名教师中分配到甲学校的人数,求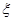 的分布列和数学期望.
的分布列和数学期望.