设函数 .
.
(1)画出函数y=f(x)的图像;
(2)若不等式 ,(a¹0,a、bÎR)恒成立,求实数x的范围.
,(a¹0,a、bÎR)恒成立,求实数x的范围.
(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分)
已知一家公司生产某种品牌服装的年固定成本为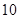 万元,每生产
万元,每生产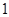 千件需另投入
千件需另投入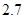 万元.设该公司一年内生产该品牌服装
万元.设该公司一年内生产该品牌服装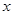 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为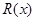 万元,且
万元,且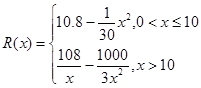
(Ⅰ)写出年利润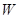 (万元)关于年产量
(万元)关于年产量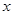 (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大,并求出最大年利润.(注:年利润=年销售收入-年总成本).
(本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分)
在如图所示的多面体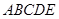 中,
中,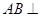 平面
平面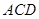 ,
, 平面
平面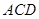 ,
,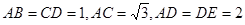 ,
,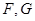 为
为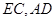 的中点.
的中点.
(Ⅰ)求证: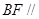 平面
平面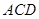 ;
;
(Ⅱ)求三棱锥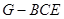 的体积.
的体积.
(本小题满分13分,(Ⅰ)小问5分,(Ⅱ)小问8分)
设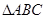 的内角
的内角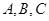 的对边分别为
的对边分别为 ,
,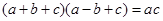 .
.
(Ⅰ)求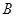 ;
;
(Ⅱ)若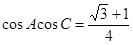 ,求
,求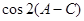 .
.
(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问3分,(Ⅲ)小问4分)
为了了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,记录了小李第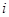 天打篮球的时间
天打篮球的时间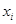 (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率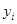 的数据,其中
的数据,其中 .
.
算得: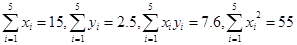 .
.
(Ⅰ)求投篮命中率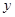 对打篮球时间
对打篮球时间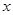 的线性回归方程
的线性回归方程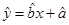 ;
;
(Ⅱ)判断变量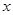 与
与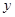 之间是正相关还是负相关;
之间是正相关还是负相关;
(Ⅲ)若小李明天准备打球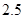 小时,预测他的投篮命中率.
小时,预测他的投篮命中率.
附:线性回归方程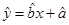 中
中 ,其中
,其中 为样本平均数.
为样本平均数.
(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分)
已知等差数列 满足:
满足: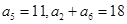 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若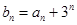 ,求数列
,求数列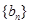 的前
的前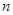 项和
项和 .
.