某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费.某顾客刚好消费200元.
(1)该顾客至少可得到 元购物券,至多可得到 元购物券;(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
“全民阅读”深入人心,读好书让人终身受益.为打造书香校园,满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和科技阅读两类图书.经了解,20本文学名著和40本科技阅读共需1520元,一本文学名著比一本科技阅读多22元(注:所采购的文学名著书价格都一样,所采购的科技阅读书价格都一样).
(1)求每本文学名著和科技阅读各多少元?
(2)若学校要求购买科技阅读比文学名著多20本,科技阅读和文学名著总数不低于72本,总费用不超过2000元,请你为学校求出符合条件的购书方案.
(3)请在(2)的条件下,请你求出此次活动学校最多需投入资金多少元?
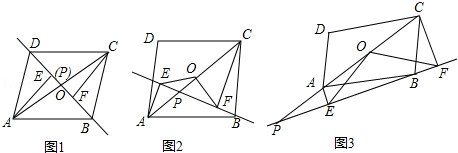
已知:点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BD作垂线,垂足分别为点E、F,点O为AC的中点.
(1)当点P与点O重合时如图1,易证 (不需证明)
(2)直线BP绕点B逆时针方向旋转,当 时,如图2、图3的位置,猜想线段CF、AE、OE之间有怎样的数量关系?请写出你对图2、图3的猜想,并选择一种情况给予证明.
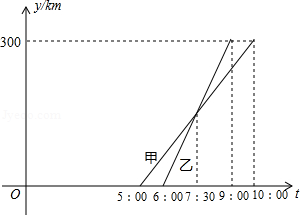
甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距 离y与时刻t的对应关系,如图所示:
(1)A、B两城之间的距离是多少千米?
(2)求乙车出发后几小时追上甲车?
(3)直接写出甲车出发后多长时间,两车相距20千米.
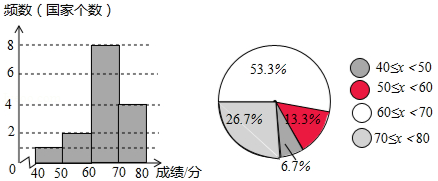
下面是某年参加国家教育评估的学校学生的数学平均成绩(x)的统计图,请根据所给信息,解答下列问题:
(1)本次共调查 所学校.
(2) 图能更好地说明一半以上学校的学生数学平均成绩在 之间.
(3)估计我国150所学校中学生的数学平均成绩在 的学校有多少所?
已知:抛物线 与x轴交于点A(2,0)、B(4,0),且过点C(0,4).
(1)求出抛物线的解析式和顶点坐标.
(2)请你求出抛物线向左平移3个单位,再向上平移1.5个单位后抛物线的解析式.
