如图，抛物线y=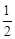
x2＋bx＋c与y轴交于点C，与x轴相交于A，B两点，点A的坐标为(2，0)，点C的坐标为(0，―4)．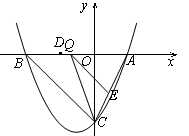
（1）求抛物线的解析式；
（2）点Q是线段OB上的动点，过点Q作QE//BC，交AC于点E，连接CQ，设OQ=m，当△CQE的面积最大时，求m的值，并写出点Q的坐标．
（3）若平行于x轴的动直线，与该抛物线交于点P，与直线BC交于点F，D的坐标为(－2，0)，则是否存在这样的直线l，使OD=DF？若存在，求出点P的坐标；若不存在，请说明理由．
如图，有一路灯杆AB（底部B不能直接到达），在灯光下，小明在点D处测得自己的影长DF＝3m，沿BD方向到达点F处再测得自己得影长FG＝4m，如果小明得身高为1.6m，求路灯杆AB的高度。
如图，△ABC中，EF∥BC，FD∥AB，AE＝18，BE＝12，CD＝14，求线段EF的长．
两个相似三角形的一对对应边的长分别是35cm和14cm，它们的周长相差60cm，求这两个三角形的周长．
在如图所附的格点图中画出两个相似的三角形.
如图，正方形EFGH的顶点在边长为a的正方形ABCD的边上，若AE=x，正方形EFGH的面积为y.
(1)求出y与x之间的函数关系式；
(2)正方形EFGH有没有最大面积？若有，试确定E点位置；若没有，说明理由.