如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC= ,直线y=
,直线y= 经过点C,交y轴于点G,且∠AGO=30°。
经过点C,交y轴于点G,且∠AGO=30°。
(1)点C、D的坐标
(2)求顶点在直线y= 上且经过点C、D的抛物线的解析式;
上且经过点C、D的抛物线的解析式;
(3)将(2)中的抛物线沿直线y= 平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请说明理由。
(本题10分,每小题5分)
(1)计算: 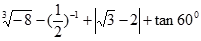 ;
;
(2)解方程组: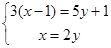
(本小题满分9分)如图,对称轴为直线x=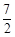 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).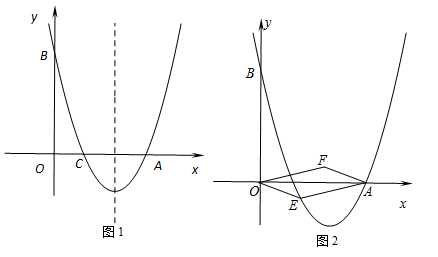
(1)求抛物线的解析式及抛物线与x轴的另一交点C的坐标;
(2)D为坐标平面上一点,且以A、B、C、D为顶点的四边形是平行四边形,写出点D的坐标;
(3)如图2,点E(x,y)是抛物线上位于第四象限的一点,四边形OEAF是以OA为对角线的平行四边形.
①当□OEAF的面积为24时,请判断□OEAF是矩形吗?是菱形吗?
②是否存在点E,使□OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
(本小题满分9分)如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0)、(12,6),直线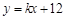 与y轴交于点P,与边OA交于点D,与边BC交于点E.
与y轴交于点P,与边OA交于点D,与边BC交于点E.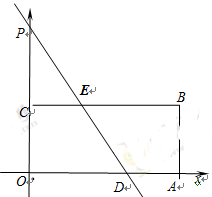
(1)若 ,求k的值;
,求k的值;
(2)在(1)的条件下,当直线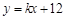 绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在NO平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;
绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在NO平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;
(3)在(1)的条件下,将矩形OABC沿DE折叠,若点O落在边BC上,求出该点坐标;若不在边BC上,求将(1)中的直线沿y轴怎样平移,使矩形OABC沿平移后的直线折叠,点O恰好落在边BC上.
(本小题满分9分)如图,已知A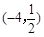 ),B(﹣1,2)是一次函数
),B(﹣1,2)是一次函数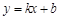 与反比例函数
与反比例函数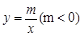 图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.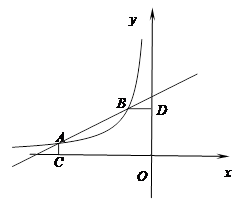
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.
(本小题满分8分)我市为治理污水,某地需要铺设一段全长为300 m的污水排放管道.铺设120 m后,为了尽量减少施工对我市交通所造成的影响,后来每天的工效比原计划增加20%,结果共用30天完成这一任务.求原计划每天铺设管道的长度.