如图所示,水平放置的平行板电容器,原来两板不带电,上极板接地,它的极板长L = 0.1m,两板间距离 d = 0.4 cm,有一束相同的带电微粒以相同的初速度先后从两板中央平行极板射入,由于重力作用微粒能落到下板上,微粒所带电荷立即转移到下极板且均匀分布在下极板上。设前一微粒落到下极板上时后一微粒才能开始射入两极板间。已知微粒质量为 m = 2×10-6kg,电量 q = 1×10-8 C,电容器电容为 C =10-6 F,取 g=10m/s2.求:(1)为使第一个微粒的落点范围能在下板中点到紧靠边缘的 B 点之内,求微粒入射的初速度 v0 的取值范围;(2)若带电微粒以第一问中初速度 v0 的最小值入射,则最多能有多少个带电微粒落到下极板上?
如图所示,一带电的小球从P点自由下落,P点距场区边界MN高为h,边界MN下方有方向竖直向下、电场场强为E的匀强电场,同时还有匀强磁场,小球从边界上的a点进入电场与磁场的复合场后,恰能作匀速圆周运动,并从边界上的b点穿出,已知ab=L,求:(1)该匀强磁场的磁感强度B的大小和方向;(2)小球从P经a至b时,共需时间为多少?
一水平传送带以v1=2m/s的速度匀速运动,将一粉笔头无初速度放在传送带上,达到相对静止时产生的划痕长L1=4m。现在让传送带以a2=1.5m/s2的加速度减速,在刚开始减速时将该粉笔头无初速度放在传送带上,(取g=10m/s2)求:
(1)粉笔头与传送带之间的动摩擦因数μ=?
(2)粉笔头与传送带都停止运动后,粉笔头离其传输带上释放点的距离L2。
如图所示,粗糙弧形轨道和两个光滑半圆轨道组成翘尾巴的S形轨道.光滑半圆轨道半径为R,两个光滑半圆轨道连接处CD之间留有很小空隙,刚好能够使小球通过,CD之间距离可忽略.粗糙弧形轨道最高点A与水平面上B点之间的高度为h.从A点静止释放一个可视为质点的小球,小球沿翘尾巴的S形轨道运动后从E点水平飞出,落到水平地面上,落点到与E点在同一竖直线上B点的距离为s.已知小球质量m,不计空气阻力,求:
(1)小球从E点水平飞出时的速度大小;
(2)小球运动到半圆轨道的B点时对轨道的压力;
(3)小球沿翘尾巴S形轨道运动时克服摩擦力做的功.
宇航员在地球表面以一定初速度竖直上抛一小球,经过时间t小球落回原处;若他在某星球表面以相同的初速度竖直上抛同一小球,需经过时间5t小球落回原地.(取地球表面重力加速度g=10 m/s2,阻力不计)
(1)求该星球表面附近的重力加速度g′;
(2)已知该星球的半径与地球半径之比为R星∶R地=1∶4,求该星球的质量与地球质量之比M星∶M地.
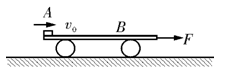
如图所示,物体A的质量为M=1 kg,静止在光滑水平面上的平板车B的质量为m=0.5 kg、长为L=1 m.某时刻物体A以v0=4 m/s向右的初速度滑上平板车B的上表面,在A滑上B的同时,给B施加一个水平向右的拉力.忽略物体A的大小,已知A与B之间的动摩擦因数为μ=0.2,取重力加速度g=10 m/s2.试求:如果要使A不至于从B上滑落,拉力F应满足的条件.