如图所示的装置是一个高真空玻璃管,管中封有若干个金属电池,电极C是阴极,电子由此射出,电极A是阳极,保持在一高的正电位上,大多数电子都打到电极A,但是电极A中有一小孔,可以使一部分电子通过,这些穿过小孔的电子又被另一电极Aˊ所限制,Aˊ上有另一小孔,所以只有一细束的电子可以通过P与Pˊ两极板间的区域,电子通过这两极板区域后打到管的末端,使末端S处的荧光物质发光。水平放置的偏转板相距为d,长度为L,它的右端与荧光右端的距离为D。(1)当偏转板上不加电场和磁场时,电子水平打到荧光屏的O点;(2)当两偏转极板只加一匀强电场(场强为E)时,在荧光屏上S点出现一亮点,测出OS=H;(3)当偏转板中又加一垂直纸面向里的匀强磁场(磁感应强度为B)时发现电子又打到荧光屏的O点。若不考虑电子的重力,且荧光屏球面的曲率半径很大,可以近似视为平面。试根据上述测量数据求出电子的荷质比e/m。 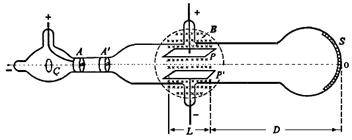
如图所示,质量m=1 kg的小球用细线拴住,线长l=0.5 m,细线所受拉力达到F=18 N时就会被拉断.当小球从图示位置释放后摆到悬点的正下方时,细线恰好被拉断。若此时小球距水平地面的高度h=5 m,重力加速度g=10 m/s2,求小球落地处到地面上P点的距离.(P点在悬点的正下方)
m/s2,求小球落地处到地面上P点的距离.(P点在悬点的正下方)
如图所示,物体的质量 ,用与竖直方向成
,用与竖直方向成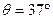 的斜向右上方的推力
的斜向右上方的推力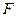 把该物体压在竖直墙壁上,并使它沿墙壁在竖直方向上做匀速直线运动。物体与墙壁间的动摩擦因数
把该物体压在竖直墙壁上,并使它沿墙壁在竖直方向上做匀速直线运动。物体与墙壁间的动摩擦因数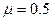 ,取重力加速度
,取重力加速度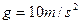 ,求推力
,求推力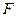 的大小。(
的大小。(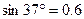 ,
, )
)
在平直的高速公路上,一辆汽车正以 的速度匀速行驶,因前方出现紧急情况,司机立即刹车,直到汽车停下,已知汽车的质量为
的速度匀速行驶,因前方出现紧急情况,司机立即刹车,直到汽车停下,已知汽车的质量为 ,刹车时汽车所受的阻力大小为
,刹车时汽车所受的阻力大小为 ,求:
,求:
(1)刹车时汽车的加速度大小;
(2)从开始刹车到最终停下,汽车运动的时间;
(3)从开始刹车到最终停下,汽车前进的距离。
计划发射一颗距离地面高度为地球半径R0的圆形轨道地球卫星,卫星轨道平面与赤道平面重合,卫星 绕地旋转方向与地球自转方向相同,已知地球表面重力加速度为g,地球自转周期T0,
绕地旋转方向与地球自转方向相同,已知地球表面重力加速度为g,地球自转周期T0,
(1)求出卫星绕地心运动的速度v和周期T
(2)赤道上的人在无遮挡的情况下,能连续看到该卫星的最长时间是多少?
质量为m=1kg的小物块轻轻放在水平匀速运动的传送带上的P点,随传送带运动到A点后水平抛出,小物块恰好无碰撞的沿圆弧切线从B点进入竖直光滑圆孤轨道下滑。B、C为圆弧的两端点,其连线水平。已知圆弧半径R=1.0m圆弧对应圆心角 ,轨道最低点为O,A点距水平面的高度h=0.8m,小物块离开C点后恰能无碰撞的沿固定斜面向上运
,轨道最低点为O,A点距水平面的高度h=0.8m,小物块离开C点后恰能无碰撞的沿固定斜面向上运 动,0.8s后经过D点,物块与斜面间的滑动摩擦因数为
动,0.8s后经过D点,物块与斜面间的滑动摩擦因数为 =
= (g=10m/s2,sin37°=0.6,cos37°=0.8)试求:
(g=10m/s2,sin37°=0.6,cos37°=0.8)试求:
|
(1)小物块离开A点的水平初速度v1。
(2)小物块经过O点时对轨道的压力。 小物块与传送带间的动摩擦因数为
小物块与传送带间的动摩擦因数为 0.3,传送带的速度为5m/s,则PA间的距离是多少?
0.3,传送带的速度为5m/s,则PA间的距离是多少?