阅读下列材料:点A、点B在数轴上分别表示两个有理数,A、B两点时间的距离表示为AB。
(1)当点A在原点时,若点B表示的数为5时,则AB=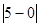 =5;若点B表示的数为﹣5时,则AB=
=5;若点B表示的数为﹣5时,则AB=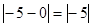 =5;若点B表示的数为a时,则AB=
=5;若点B表示的数为a时,则AB=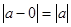 ,当a>0, AB=a,当a=0,AB=0,当a<0,AB=-a
,当a>0, AB=a,当a=0,AB=0,当a<0,AB=-a
(2)当A、B都不在原点时,A表示的数为a,B表示的数为b,则AB=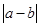 ,当a-b>0时,AB=
,当a-b>0时,AB=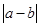 =a﹣b;当a-b=0时,AB=
=a﹣b;当a-b=0时,AB=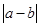 =0;当a-b<0时,AB=
=0;当a-b<0时,AB=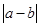 =﹣(a﹣b)=﹣a﹢b。
=﹣(a﹣b)=﹣a﹢b。
根据上述材料,回答下列问题:
有理数a、b、c在数轴上的位置如图所示:
化简(1)
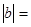
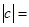

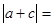
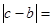

化简(2)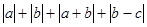
如图,在 中, , 是 的中点, 与 相切于点 , 交 于点
(1)求证: 是 的切线;
(2)若 ,点 是 上一个动点(不与 , 两点重合),求 的度数.
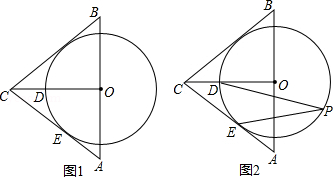
为了维护国家主权和海洋权利,我国海监部门对中国海域实现常态化管理.某日,我国海监船在某海岛附近的海域执行巡逻任务.如图,此时海监船位于海岛 的北偏东 方向,距离海岛100海里的 处,它沿正南方向航行一段时间后,到达位于海岛 的南偏东 方向的 处,求海监船航行了多少海里(结果保留根号)?
列方程解应用题
某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮的传播就会有144台电脑被感染,请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?
如图,四边形 是正方形,点 , 分别在 , 上,且 .
求证: .
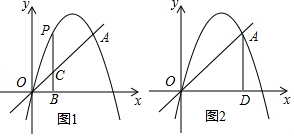
已知:如图,抛物线 经过原点 和点 , 为抛物线上的一个动点,过点 作 轴的垂线,垂足为 ,并与直线 交于点 .
(1)求抛物线的解析式;
(2)当点 在直线 上方时,求线段 的最大值;
(3)过点 作 轴于点 ,在抛物线上是否存在点 ,使得以 、 、 、 四点为顶点的四边形是平行四边形?若存在,求 的值;若不存在,请说明理由.