如图一,在Rt△ABC中,∠ACB=90°,∠A=30°,P为BC边上任意一点,点Q为AC边动点,分别以Cm、MQ为边做等边△MPF和等边△PQE,连接EF.
(一)试探索EF与AB位置关系,并证明;
(5)如图5,当点P为BC延长线上任意一点时,(一)结论是否成立?请说明理由.
(3)如图3,在Rt△ABC中,∠ACB=90°,∠A=m°,P为BC延长线上一点,点Q为AC边动点,分别以CP、PQ为腰做等腰△PCF和等腰△PQE,使得PC=PF,PQ=PE,连接EF.要使(一)的结论依然成立,则需要添加怎样的条件?为什么?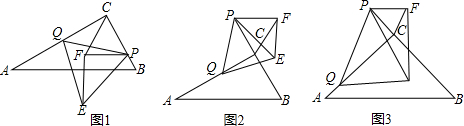
利用计算器计算这组数的平均数:1576 1573 1564 1708 1625 1594 1478 1479 1625 1601 1785 1432 1597 1591 1602 1701
某中学为了了解全校的耗电情况,抽查了10 天中全校每天的耗电量,数据如下表:(单位:kW·h)
| 耗电量/kW·h) |
90 |
93 |
102 |
113 |
114 |
120 |
| 天数 |
1 |
1 |
2 |
3 |
1 |
2 |
(1)写出上表中数据的众数和平均数;
(2)由上题获得的数据,估计该校某月的耗电量(按30天计);
(3)若当地每度电的定价是0.5元,写出该校应付电费y(元)与天数x 之间的函数关系式.
某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售如下:
| 每人销售件数 |
1800 |
510 |
250 |
210 |
150 |
120 |
| 人数 |
1 |
1 |
3 |
5 |
3 |
2 |
(1)求这15位营销人员该月销售量的平均数、中位数和众数.
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你制定一个合理的销售定额,并说明理由.
在一次数学测验中,30名学生的成绩如下表所示:
| 分数 |
75 |
80 |
88 |
92 |
96 |
98 |
100 |
| 人数 |
2 |
3 |
5 |
11 |
7 |
1 |
1 |
求这组数据的众数和中位数.
公园里有甲、乙两群游客正在做团体游戏,两群游客的年龄如下(单位:岁):
甲群:13,13,14,15,15,15,15,16,17,17;
乙群:3,4,4,5,5,6,6,6,54,57.
(1)甲群游客的平均年龄是多少?中位数、众数呢? 其中能较好反映甲群游客年龄特征的是什么?
(2)乙群游客的平均年龄是多少?中位数、众数呢? 其中能较好反映乙群游客年龄特征的是什么?