某中学为了了解全校的耗电情况,抽查了10 天中全校每天的耗电量,数据如下表:(单位:kW·h)
| 耗电量/kW·h) |
90 |
93 |
102 |
113 |
114 |
120 |
| 天数 |
1 |
1 |
2 |
3 |
1 |
2 |
(1)写出上表中数据的众数和平均数;
(2)由上题获得的数据,估计该校某月的耗电量(按30天计);
(3)若当地每度电的定价是0.5元,写出该校应付电费y(元)与天数x 之间的函数关系式.
为加强中小学生安全教育,某校组织了“防溺水”知识竞赛,对表现优异的班级进行奖励,学校购买了若干副乒乓球拍和羽毛球拍.购买2副乒乓球拍和1副羽毛球拍共需116元;购买3副乒乓球拍和2副羽毛球拍共需204元.
(1)求购买1副乒乓球拍和1副羽毛球拍各需多少元;
(2)若学校购买乒乓球拍和羽毛球拍共30副,且支出不超过1480元,则最多能够购买多少副羽毛球拍?
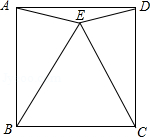
如图,四边形 是正方形, 是等边三角形.
(1)求证: ;
(2)求 的度数.
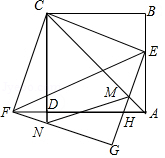
如图,正方形 的边长为1,点 为边 上一动点,连接 并将其绕点 顺时针旋转 得到 ,连接 ,以 、 为邻边作矩形 , 与 、 分别交于点 、 , 交 延长线于点 .
(1)证明:点 、 、 在同一条直线上;
(2)随着点 的移动,线段 是否有最小值?若有,求出最小值;若没有,请说明理由;
(3)连接 、 ,当 时,求 的长.
如图, 的顶点 、 分别在 轴, 轴上, ,且 的面积为8.
(1)直接写出 、 两点的坐标;
(2)过点 、 的抛物线 与 轴的另一个交点为点 .
①若 是以 为腰的等腰三角形,求此时抛物线的解析式;
②将抛物线 向下平移4个单位后,恰好与直线 只有一个交点 ,求点 的坐标.

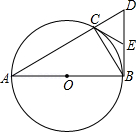
如图,已知 内接于 , 为 的直径, ,交 的延长线于点 .
(1) 为 的中点,连接 ,求证: 是 的切线;
(2)若 ,求 的大小.