计算: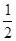 +(-
+(-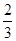 )+
)+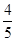 +(-
+(-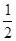 )+(-
)+(-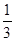 );
);
(11·漳州)(满分13分)如图,直线y=-2x+2与x轴、y轴分别交于A、B两点,将△OAB绕点O逆时针方向旋转90°后得到△OCD.
(1)填空:点C的坐标是(_▲,_ ▲),
▲),
点D的坐标是(_▲,_▲);
(2)设直线CD与AB交于点M,求线段BM的长;
(3)在y轴上是否存在点P,使得△BMP是等腰三角形?若存在,
请求出所有满足条件的点P的坐标;若不存在,请说明理由.
(11·漳州)(满分10分)2008年漳州市出口贸易总值为22.52亿美元,至2010年出口贸易总值达到50.67亿美元,反映了两年来漳州市出口贸易的高速增长.
(1)求这两年漳州市出口贸易的年平均增长率;
(2)按这样的速度增长,请你预测2011年漳州市的出口贸易总值.
(温馨提示:2252=4×563,5067=9×563)
(11·漳州)(满分10分)如图,AB是⊙O的直径,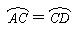 ,∠COD=60°.
,∠COD=60°.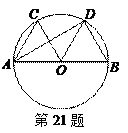
(1)△AOC是等边三角形吗?请说明理由;
(2)求证:OC∥BD.
(11·漳州)(满分8分)某校“我爱学数学”课题学习小组的活动主题是“测量学校旗杆的高度”.以下是该课题小组研究报告的部分记录内容:
| 课题 |
测量学校旗杆的高度 |
| 图示 |
 |
| 发言记录 |
小红:我站在远处看旗杆顶端,测得仰角为30° 小亮:我从小红的位置向旗杆方向前进12 m看旗杆顶端,测得仰角为60° 小红:我和小亮的目高都是1.6 m |
请你根据表格中记录的信息,计算旗杆AG的高度.(取1.7,结果保留两个有效数字)
(11·漳州)(满分8分)漳州市某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题: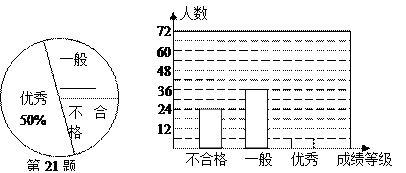
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有_▲人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?