我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题这种方法称为等面积法,这是一种重要的数学方法.请你用等面积法来探究下列两个问题: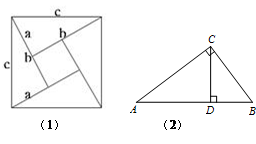
(1)如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,请你用它来验证勾股定理;
(2)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC= 4,BC=3,求CD的长度.
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=EF,∠BAC=∠DEF=90°,固定△ABC,将△EFD绕点A 顺时针旋转,当DF边与AB边重合时,旋转中止.不考虑旋转开始和结束时重合的情况,设DE、DF(或它们的延长线)分别交BC(或它的延长线)于G、H点,如图(2).
(1)问:始终与△AGC相似的三角形有 ;
(2)请选择(1)中的一组相似三角形加以证明.
如图,已知:△ABC中,∠ABC=90°,AB=BC,延长BC到E,使得CE=2BC,取CE的中点D,连接AE、AD.求证:△ACD∽△ECA.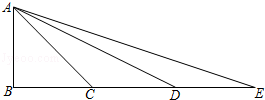
如图,在梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3.问:线段AB上是否存在点P,使得以P、A、D为顶点的三角形与以P、B、C为顶点的三角形相似?若存在,这样的总共有几个?并求出AP的长;若不存在,请说明理由.
如图,在△ABC中,∠BAC=90°,D为BC的中点,AE⊥AD,AE交CB的延长线于点E.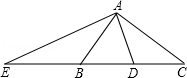
(1)求证:△EAB∽△ECA;
(2)△ABE和△ADC是否一定相似?如果相似,加以说明;如果不相似,那么增加一个怎样的条件,△ABE和△ADC一定相似.
如图,Rt△ABC,D是斜边AC上的一动点(点D不与点A、C重合),过D点作直线截△ABC,使截得的三角形与△ABC相似,请你画出满足条件的所有直线.