(本小题满分14分)某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B,要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
| |
产品A(件) |
产品B(件) |
|
| 研制成本与搭载 费用之和(万元/件) |
20 |
30 |
计划最大资金额300万元 |
| 产品重量(千克/件) |
10 |
5 |
最大搭载重量110千克 |
| 预计收益(万元/件) |
80 |
60 |
|
试问:如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
(本小题满分13分)已知椭圆C的中心在圆点,焦点在x轴上,F1,F2分别是椭圆C的左、右焦点,M是椭圆短轴的一个端点,过F1的直线 与椭圆交于A,B两点,
与椭圆交于A,B两点, 的面积为4,
的面积为4, 的周长为
的周长为 (I)求椭圆C的方程;(II)设点Q的坐标为(1,0),是否存在椭圆上的点P及以Q为圆心的一个圆,使得该圆与直线PF1,PF2都相切,若存在,求出P点坐标及圆的方程;若不存在,请说明理由。
(I)求椭圆C的方程;(II)设点Q的坐标为(1,0),是否存在椭圆上的点P及以Q为圆心的一个圆,使得该圆与直线PF1,PF2都相切,若存在,求出P点坐标及圆的方程;若不存在,请说明理由。
(本小题满分12分)如图所示,已知 中,
中, AB=2OB=4,D为AB的中点,若
AB=2OB=4,D为AB的中点,若 是
是 绕直线AO旋转而成的,记二面角B—AO—C的大小为
绕直线AO旋转而成的,记二面角B—AO—C的大小为 (I)若
(I)若 ,求证:平面
,求证:平面 平面AOB;(II)若
平面AOB;(II)若 时,求二面角C—OD—B的余弦值的最小值。
时,求二面角C—OD—B的余弦值的最小值。
(本小题满分12分)2010年广东亚运会,某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D两个动作,比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩。假设每个运动员完成每个系列中的两个动作的得分是相互独立的,根据赛前训练统计数据,某运动员完成甲系列和乙系列的情况如下表:
甲系列:
| 动作 |
K |
D |
||
| 得分 |
100 |
80 |
40 |
10 |
| 概率 |
 |
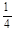 |
 |
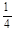 |
乙系列:
| 动作 |
K |
D |
||
| 得分 |
90 |
50 |
20 |
0 |
| 概率 |
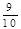 |
 |
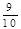 |
 |
现该运动员最后一个出场,其之前运动员的最高得分为118分。
(I)若该运动员希望获得该项目的第一名,应选择哪个系列,说明理由,并求其获得第一名的概率;
(II)(II)若该运动员选择乙系列,求其成绩X的分布列及其数学期望EX。
(本小题满分12分)已知函数 (I)求函数
(I)求函数 上的最小值;(II)求证:对一切
上的最小值;(II)求证:对一切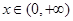 ,都有
,都有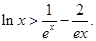
已知函数 =
=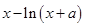 在
在 处取得极值.
处取得极值.
(1)求实数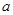 的值;
的值;
(2) 若关于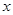 的方程
的方程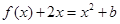 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;