(本小题满分14分)
如图,在四棱锥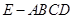 中,
中,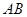 ⊥平面
⊥平面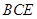 ,
,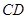 ⊥平面
⊥平面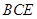 ,
,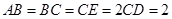 ,
,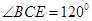 。
。
(1)求证:平面ADE⊥平面ABE;
(2)求二面角A—EB—D的余弦值.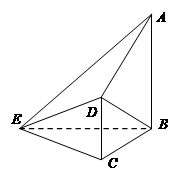
已知 .
.
(Ⅰ)求 的值;(Ⅱ)求
的值;(Ⅱ)求 的值.
的值.
已知数列 、
、 满足:
满足: .
.
(1)求证:数列 是等差数列;
是等差数列;
(2)求数列 的通项公式;
的通项公式;
(3)设 ,若
,若 对于
对于 恒成立,试求实数
恒成立,试求实数 的取值范围
的取值范围
(本小题满分13分)对于数列 ,规定数列
,规定数列 为数列
为数列 的一阶差分数列,其中
的一阶差分数列,其中 ;一般地,规定
;一般地,规定 为
为 的
的 阶差分数列,其中
阶差分数列,其中 ,且
,且 .
.
(1)已知数列 的通项公式
的通项公式 ,试证明
,试证明 是等差数列;
是等差数列;
(2)若数列 的首项
的首项 ,且满足
,且满足 ,求数列
,求数列 及
及 的通项公式;
的通项公式;
(3)在(2)的条件下,判断 是否存在最小值,若存在求出其最小值,若不存在说明理由.
是否存在最小值,若存在求出其最小值,若不存在说明理由.
.设数列 的前
的前 项和为
项和为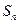 ,且满足
,且满足 (
( =1,2,3,…).
=1,2,3,…).
( 1)求数列
1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足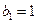 ,且
,且 ,求数列
,求数列 的通项公式;
的通项公式;
(3)设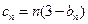 ,求数列
,求数列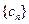 的前
的前 项和
项和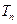 .
.
(8,9,10班学生做下面的题)
已知函数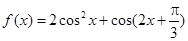
(1)若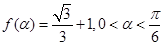 ,求
,求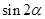 的值;
的值;
(2)在锐角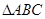 中,
中, ,
,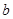 ,
,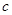 分别是角
分别是角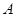 ,
, ,
, 的对边;若
的对边;若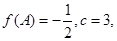
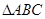 的面积
的面积 ,求
,求 的值.
的值.