(本小题满分13分)对于数列 ,规定数列
,规定数列 为数列
为数列 的一阶差分数列,其中
的一阶差分数列,其中 ;一般地,规定
;一般地,规定 为
为 的
的 阶差分数列,其中
阶差分数列,其中 ,且
,且 .
.
(1)已知数列 的通项公式
的通项公式 ,试证明
,试证明 是等差数列;
是等差数列;
(2)若数列 的首项
的首项 ,且满足
,且满足 ,求数列
,求数列 及
及 的通项公式;
的通项公式;
(3)在(2)的条件下,判断 是否存在最小值,若存在求出其最小值,若不存在说明理由.
是否存在最小值,若存在求出其最小值,若不存在说明理由.
(本小题满分12分)
已知
 R
R .
.
(1)求函数 的周期和单调减区间;
的周期和单调减区间;
(2)若 ,且
,且 ,求
,求 和
和 的值.
的值.
(本小题满分12分)设p:实数x满足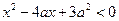 ,其中
,其中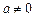 ,
,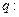 实数
实数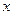 满足
满足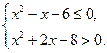
(Ⅰ)若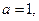 且
且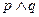 为真,求实数
为真,求实数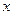 的取值范围;
的取值范围;
(Ⅱ)若┐q是┐p的必要不充分条件,求实数 的取值范围.
的取值范围.
(本小题满分12分)口袋里有分别标有数字1、2、3、4的4只白球和分别标有数字5、6的2只红球,这些球除了颜色和所标数字外完全相同.某人从中随机取出一球,记下球上所标数字后放回,再随机取出一球并记下球上所标数字,
(Ⅰ)求两次取出的球上的数字之和大于8的概率;
(Ⅱ)求两次取出的球颜色不同的概率;
(本小题满分12分)下表是种产品销售收入与销售量之间的一组数据:
| 销售量x(吨) |
2 |
3 |
5 |
6 |
| 销售收入y(千元) |
7 |
8 |
9 |
12 |
(I)画出散点图;
(II)求出回归方程;
(III)根据回归方程估计销售量为9吨时的销售收入。
(参考数据:2×7+3×8+5×9+6×12=155,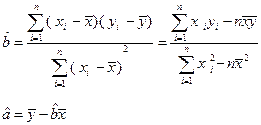 )
)
(本小题满分12分)为了了解2011年某校高三学生的视力情况,随机抽查了一部分学生视力,将调查结果分组,分组区间为(3.9,4.2],(4.2,4.5],… ,(5.1,5.4].经过数据处理,得到如下频率分布表:
| 分组 |
频数 |
频率 |
| (3.9,4.2] |
3 |
0.06 |
| (4.2,4.5] |
6 |
0.12 |
| (4.5,4.8] |
25 |
x |
| (4.8,5.1] |
y |
z |
| (5.1,5.4] |
2 |
0.04 |
| 合计 |
n |
1.00 |
(I)求频率分布表中未知量n,x,y,z的值;
(II)从样本中视力在(3.9,4.2]和(5.1,5.4]的所有同学中随机抽取两人,求两人的视力差的绝对值低于0.5的概率.