.(本小题满分14分)
已知数列 的首项
的首项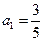 ,
,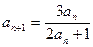 ,其中
,其中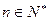 。
。
(Ⅰ)求证:数列 为等比数列;
为等比数列;
(Ⅱ)记 ,若
,若 ,求最大的正整数
,求最大的正整数 。
。
已知 向量
向量 ,设函数
,设函数
 。
。
(Ⅰ)求 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(Ⅱ)在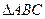 中,
中, 、
、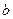 、
、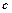 分别是角
分别是角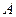 、
、 、
、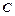 的对边,若
的对边,若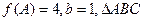 的面积为
的面积为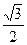 ,求
,求 的值。
的值。
已知函数 .
.
⑴若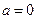 ,解方程
,解方程 ;
;
⑵若 ,求
,求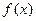 的单调区间;
的单调区间;
⑶若存在实数 ,使
,使 ,求实数
,求实数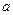 的取值范围 .
的取值范围 .
已知定义域为R的函数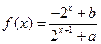 是奇函数。
是奇函数。
⑴求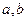 的值;并判定函数
的值;并判定函数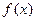 单调性(不必证明)。
单调性(不必证明)。
⑵若对于任意的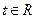 ,不等式
,不等式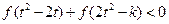 恒成立,求
恒成立,求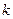 的取值范围。
的取值范围。
某租赁公司出租同一型号的设备40套,当每套月租金为270元时,恰好全部租出,在此基础上,每套月租金每增加10元,就少租出1套设备,而未租出的设备每月需支付各种费用每套20元,设每套设备实际月租金为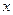
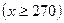 元,月收益为
元,月收益为 元(总收益=设备租金收入—未租出设备支出费用)。
元(总收益=设备租金收入—未租出设备支出费用)。
⑴求 与
与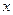 的函数关系式;
的函数关系式;
⑵当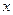 为何值时,月收益最大?最大月收益是多少?
为何值时,月收益最大?最大月收益是多少?