某租赁公司出租同一型号的设备40套,当每套月租金为270元时,恰好全部租出,在此基础上,每套月租金每增加10元,就少租出1套设备,而未租出的设备每月需支付各种费用每套20元,设每套设备实际月租金为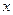
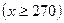 元,月收益为
元,月收益为 元(总收益=设备租金收入—未租出设备支出费用)。
元(总收益=设备租金收入—未租出设备支出费用)。
⑴求 与
与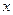 的函数关系式;
的函数关系式;
⑵当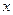 为何值时,月收益最大?最大月收益是多少?
为何值时,月收益最大?最大月收益是多少?
已知命题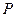 :
: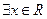 ,使
,使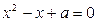 ;命题
;命题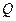 :函数
:函数 的定义域为R.(1)若命题
的定义域为R.(1)若命题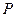 为真,求实数
为真,求实数 的取值范围;(2)若命题
的取值范围;(2)若命题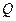 为真,求实数
为真,求实数 的取值范围;(3)如果P且 Q为假,或P或 Q为真,求实数
的取值范围;(3)如果P且 Q为假,或P或 Q为真,求实数 的取值范围.
的取值范围.
已知椭圆中心在原点,长轴在坐标轴上,离心率为 ,短轴长为4,求椭圆标准方程
,短轴长为4,求椭圆标准方程
如右图(1)所示,定义在区间 上的函数
上的函数 ,如果满
,如果满
足:对 ,
, 常数A,都有
常数A,都有 成立,则称函数
成立,则称函数 在区间
在区间 上有下界,其中
上有下界,其中 称为函数的下界. (提示:图(1)、(2)中的常数
称为函数的下界. (提示:图(1)、(2)中的常数 、
、 可以是正数,也可以是负数或零)
可以是正数,也可以是负数或零) (Ⅰ)试判断函数
(Ⅰ)试判断函数 在
在 上是否有下界?并说明理由;
上是否有下界?并说明理由;
(Ⅱ)又如具有右图(2)特征的函数称为在区间 上有上界.
上有上界.
请你类比函数有下界的定义,给出函数 在区间
在区间 上
上
有上界的定义,并判断(Ⅰ)中的函数在 上是否
上是否
有上界?并说明理由;
(Ⅲ)若函数 在区间
在区间 上既有上界又有下界,则称函数
上既有上界又有下界,则称函数 在区间
在区间 上有界,函数
上有界,函数 叫做有界函数.试探究函数
叫做有界函数.试探究函数 (
(

 是常数)是否是
是常数)是否是 (
(
 、
、 是常数)上的有界函数?
是常数)上的有界函数?
已知:三次函数 ,在
,在 上单调增,在(-1,2)上单调减,当且仅当
上单调增,在(-1,2)上单调减,当且仅当 时,
时,
|
(1)求函数f (x)的解析式;(2)若函数 ,求
,求 的单调区间.
的单调区间.
在△ABC中,角A、B、C的对边分别为a、b、c,若
(1)求证:A=B;(2)求边长c的值;(3)若 求△ABC的面积.
求△ABC的面积.