设 是定义在
是定义在 上以2为周期的函数,对
上以2为周期的函数,对 ,用
,用 表示区间
表示区间 .
.
已知当 时,函数
时,函数 .
.
(1)求 在
在 上的解析式;
上的解析式;
(2)对自然数 ,求集合
,求集合 {
{ 使方程
使方程 在
在 上有两个不相等的实根}
上有两个不相等的实根}
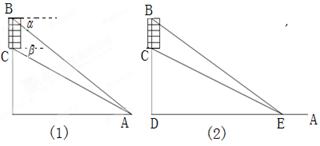
如图,山顶有一座石塔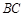 ,已知石塔的高度为
,已知石塔的高度为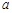 .
.
(1)若以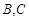 为观测点,在塔顶
为观测点,在塔顶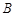 处测得地面上一点
处测得地面上一点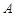 的俯角为
的俯角为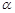 ,在塔底
,在塔底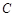 处测得
处测得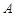 处的俯角为
处的俯角为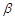 ,用
,用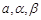 表示山的高度
表示山的高度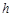 ;
;
(2)若将观测点选在地面的直线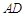 上,其中
上,其中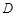 是塔顶
是塔顶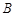 在地面上的射影. 已知石塔高度
在地面上的射影. 已知石塔高度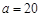 ,当观测点
,当观测点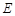 在
在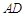 上满足
上满足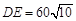 时看
时看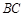 的视角(即
的视角(即 )最大,求山的高度
)最大,求山的高度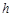 .
.
已知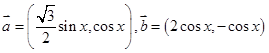 ,函数
,函数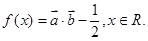
(1)求函数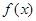 的最小值和最小正周期;
的最小值和最小正周期;
(2)设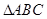 的内角
的内角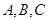 的对边分别为
的对边分别为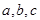 ,且
,且 ,
, ,若
,若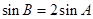 ,求
,求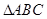 的面积.
的面积.
等比数列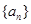 的前
的前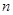 项和为
项和为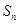 ,公比
,公比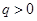 ,已知
,已知 .
.
(1)求数列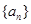 的通项公式;
的通项公式;
(2)若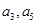 分别为等差数列
分别为等差数列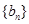 的第4项和第16项,试求数列
的第4项和第16项,试求数列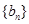 的通项公式及前
的通项公式及前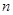 项和
项和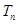 .
.
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.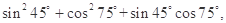
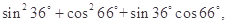
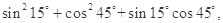
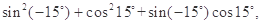
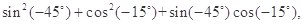
(1)试从上述五个式子中选择一个,求出这个常数;
(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
已知关于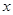 的不等式
的不等式 的解集为
的解集为 .
.
(1)求实数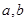 的值;
的值;
(2)解关于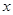 的不等式:
的不等式: (
( 为常数).
为常数).