如图，在等腰梯形OABC中，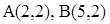
.直线
（t>0）由点O向点C移动，至点C完毕，记扫描梯形时所得直线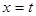
左侧的图形面积为
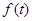.试求
的解析式，并画出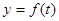
的图像.
我国西南地区正遭受着百年不遇的旱灾．据气象预报，未来48小时受灾最严重的甲地有望迎来一次弱降雨过程．某军区命令M
部队立即前往甲地准备实施人工增雨作业，已知“人工增雨”高炮车Ⅰ号载有3枚“增雨炮弹”和1枚“增雨火箭”，通过炮击“积雨云”实施增雨，第一次击中积雨云只能使云层中的水分子凝聚，第二次击中同一积雨云才能成功增雨．如果需要第4次射击才使用“增雨火箭”，当增雨成功或者增雨弹用完才停止射击．每次射击相互独立，且用“增雨炮弹
”击中积雨云的概率是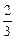
，用“增雨火箭”击中积雨云的概率是
．
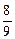（Ⅰ）
求不使用“增雨火箭”就能成功增雨的概率；
（Ⅱ）求要使用“增雨火箭”才能成功增雨的概率；
（Ⅲ）求射击次数不小于3的概率．
如图，在四棱锥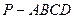
中，
，
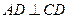，且DB平分
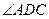，E为PC的中点，
,
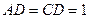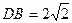
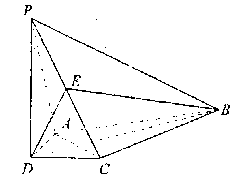
（Ⅰ）证明
;
（Ⅱ）证明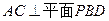
;
（Ⅲ）求直线BC与平面PBD所成的角的正切值
等差数列{an }中，
=30，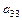
=15，求使an≤0的最小自然数n.
△ABC中，角A，B，C对边的边长分别是a，b，c，且a(cosB＋cosC)＝b＋c.
(1)求证：A＝；
(2)若△ABC外接圆半径为1，求△ABC周长的取值范围．
设椭圆
：
的左、右焦点分别为
、
，上顶点为
，在
轴负半轴上有一点
，满足
，且
⊥
．
（Ⅰ）求椭圆的离心率；
（Ⅱ）若过、、三点的圆恰好与直线
相切，求椭圆的方程；
（Ⅲ）在（Ⅱ）的条件下，过右焦点作斜率为
的直线
与椭圆交于
、
两点，
若点
使得以
为邻边的平行四边形是菱形，求
的取值范围．