△ABC中,角A,B,C对边的边长分别是a,b,c,且a(cosB+cosC)=b+c.
(1)求证:A=;
(2)若△ABC外接圆半径为1,求△ABC周长的取值范围.
.(12分)已知正方体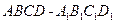 .(Ⅰ)求证:平面
.(Ⅰ)求证:平面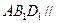 平面
平面 ;
;
(Ⅱ)求直线 与
与 所成角的大小.
所成角的大小.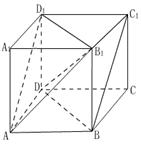
(12分)已知三角形ABC的顶点坐标为
A(-1,5)、B(-2,-1)、C(4,3),M是BC边
的中点.
(I)求AB边所在的直线方程;
(II)求中线AM的长.
(10分)已知函数 ,且
,且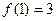 .(I)求
.(I)求 的值;(II)求函数
的值;(II)求函数 在[1,3]上的最小值和最大值.
在[1,3]上的最小值和最大值.
椭圆G: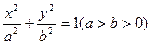 的两个焦点
的两个焦点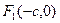 、
、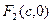 ,M是椭圆上一点,且满足
,M是椭圆上一点,且满足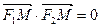 .
.
(1)求离心率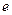 的取值范围;
的取值范围;
(2)当离心率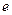 取得最小值时,点
取得最小值时,点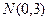 到椭圆上的点的最远距离为
到椭圆上的点的最远距离为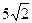 ;
;
①求此时椭圆G的方程;
②设斜率为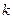 (
(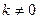 )的直线
)的直线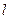 与椭圆G相交于不同的两点A、B,Q为AB的中点,问:A、B两点能否关于过点
与椭圆G相交于不同的两点A、B,Q为AB的中点,问:A、B两点能否关于过点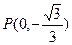 、Q的直线对称?若能,求出
、Q的直线对称?若能,求出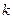 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.
已知函数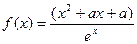 ,(
,(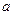 为常数,
为常数,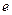 为自然对数的底).
为自然对数的底).
(1)令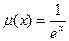 ,
,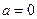 ,求
,求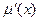 和
和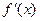 ;
;
(2)若函数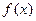 在
在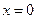 时取得极小值,试确定
时取得极小值,试确定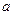 的取值范围;
的取值范围;
[理](3)在(2)的条件下,设由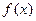 的极大值构成的函数为
的极大值构成的函数为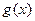 ,试判断曲线
,试判断曲线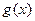 只可能与直线
只可能与直线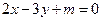 、
、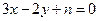 (
(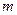 ,
,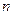 为确定的常数)中的哪一条相切,并说明理由.
为确定的常数)中的哪一条相切,并说明理由.